2020-05-25
320
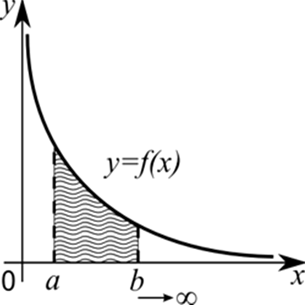
1. Интегральная сумма и ее предел. Понятие определенного интеграла. Теорема существования. Геометрический смысл.
2. Свойства определенного интеграла.
3. Теорема о среднем.
4. Интеграл с переменным верхним пределом.
5. Формула Ньютона-Лейбница.
6. Интегрирование по частям для определенного интеграла.
7. Замена переменной в определенном интеграле.
8. Вычисление площадей с помощью определенного интеграла.
9. Вычисление объёмов тел, в том числе тел вращения.
10. Длина дуги. Дифференциал длины дуги.
11. Вычисление длины кривой, заданной в декартовых координатах.
Задачи для проведения промежуточного контроля усвоения материала раздела «Определенный интеграл»
Задание1. Вычислить определенные интегралы.
1. 1)  ;
| 2. 1)  ;
|
2)  ;
| 2)  ;
|
3)  .
| 3)  .
|
3. 1) 
| 4. 1)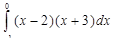 
|
2) 
| 2) 
|
3)  .
| 3)  .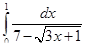
|
5. 1) 
| 6.1) 
|
2) 
| 2) 
|
3) 
| 3) 
|
7. 1) 
| 8. 1) 
|
2) 
| 2) 
|
3) 
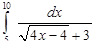
| 3) 
|
9. 1) 
| 10. 1) 
|
2)  ;
| 2)  ;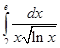
|
3)  .
| 3)  .
|
Задание 2. Вычислить площадь фигуры, ограниченной параболой и прямой. Сделать чертеж.
1. 
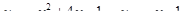
| 2. 
|
3. 
| 4.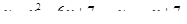 
|
5. 
| 6. 
|
7. 
| 8. 
|
9. 
| 10. 
|
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
|
|
|
Цель курса. Изучить поведение интегралов с бесконечными пределами и от неограниченных функций.
При введении понятия определенного интеграла мы исходили из условий ограниченности подынтегральной функции и конечности пределов интегрирования. Такой интеграл называется собственным (слово «собственный» обычно опускается). Если хотя бы одно из этих двух условий не выполнено, то интеграл называется несобственным.
Интегралы с бесконечными пределами интегрирования.
|
|
Пусть функция 
определена и непрерывна при всех значениях 
.
Определение 1. Если существует конечный предел
то этот предел называется
несобственным интегралом с бесконечным верхним пределом интегрирования от функции на интервале 
и обозначается
Определение 2. Если предел (22) существует и конечен, то несобственный интеграл называется сходящимся, если же предел бесконечен или не существует – расходящимся.
