Если правая часть уравнения 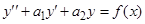 представляет собой сумму двух функций
представляет собой сумму двух функций 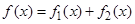 , а
, а 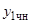 и
и 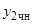 — частные решения уравнений
— частные решения уравнений  и
и  , то функция
, то функция 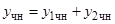 является частным решением данного уравнения.
является частным решением данного уравнения.
Пример 8. Найти методом неопределенных коэффициентов общее решение дифференциального уравнения:
1)  ; 2)
; 2) 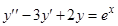 ; 3)
; 3)  .
.
Решение.
1)  . Общее решение неоднородного уравнения имеет вид:
. Общее решение неоднородного уравнения имеет вид: 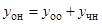 . Сначала найдем решение
. Сначала найдем решение 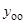 однородного уравнения
однородного уравнения 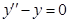 . Характеристическое уравнение
. Характеристическое уравнение 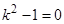 имеет корни
имеет корни  ,
, 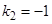 , следовательно
, следовательно  (табл. 1).
(табл. 1).
Теперь найдем частное решение неоднородного уравнения 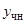 . Правая часть имеет вид:
. Правая часть имеет вид:
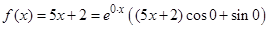 .
.
Сравниваем с формулой (20), определяем, что 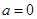 ,
, 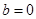 , значит контрольное число
, значит контрольное число 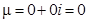 , оно не совпадает с корнями характеристического уравнения.
, оно не совпадает с корнями характеристического уравнения. 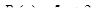 ,
, 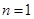 , следовательно
, следовательно 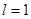 . Согласно формуле (21), частное решение имеет вид:
. Согласно формуле (21), частное решение имеет вид:
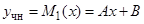 .
.
Для нахождения 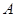 и
и 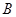 подставим
подставим 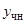 в исходное уравнение
в исходное уравнение  и приравняем коэффициенты при одинаковых степенях x. Это удобно делать с помощью таблицы, в которой слева записывают частное решение и его производные с их коэффициентами, справа — выражения этих функций через неизвестные коэффициенты А и В.
и приравняем коэффициенты при одинаковых степенях x. Это удобно делать с помощью таблицы, в которой слева записывают частное решение и его производные с их коэффициентами, справа — выражения этих функций через неизвестные коэффициенты А и В.
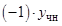
| 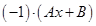
|

| 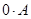
|
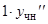
| 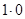
|
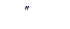
| 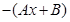
|
Просуммированные строки приравниваем к правой части  , получаем
, получаем
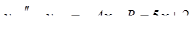 .
.
Затем приравниваем коэффициенты при одинаковых степенях 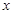 :
:
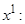
| 
|
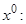
| 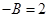
|
Тогда 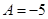 ,
, 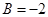 , следовательно
, следовательно 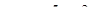 . Запишем общее решение неоднородного уравнения в виде суммы
. Запишем общее решение неоднородного уравнения в виде суммы 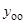 и
и 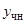 .
.
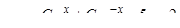 .
.
2) 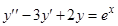 . Найдем решение
. Найдем решение 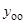 однородного уравнения
однородного уравнения 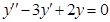 . Характеристическое уравнение
. Характеристическое уравнение  имеет корни
имеет корни  ,
,  , следовательно
, следовательно  (табл. 1).
(табл. 1).
Найдем частное решение 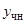 . Правая часть имеет вид
. Правая часть имеет вид  , следовательно
, следовательно 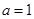 ,
, 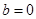 , контрольное число
, контрольное число 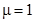 , оно совпадает с одним из корней характеристического уравнения
, оно совпадает с одним из корней характеристического уравнения  .
. 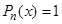 ,
, 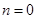 , следовательно
, следовательно 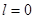 , и согласно формуле (22), частное решение имеет вид:
, и согласно формуле (22), частное решение имеет вид:
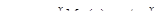 .
.
Для нахождения 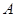 подставим
подставим 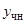 в исходное уравнение
в исходное уравнение 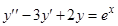 .
.

| 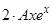
|

| 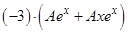
|
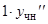
| 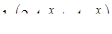
|
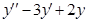
| 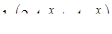 + + 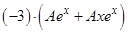 + + 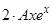
|
Просуммированные строки приравниваем к правой части  , получаем
, получаем
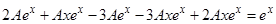 .
.
Сократим выражение на  и приведем подобные:
и приведем подобные:
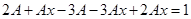 ;
;
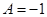 .
.
Следовательно,  . Запишем общее решение неоднородного уравнения:
. Запишем общее решение неоднородного уравнения:
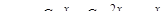 .
.
3)  . Найдем решение
. Найдем решение 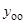 однородного уравнения
однородного уравнения 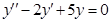 . Характеристическое уравнение
. Характеристическое уравнение  имеет корни
имеет корни  , следовательно
, следовательно
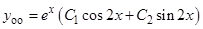 .
.
Найдем частное решение 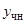 . Правая часть
. Правая часть 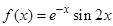 , следовательно,
, следовательно, 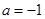 ,
, 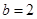 , контрольное число
, контрольное число 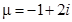 . Его нет среди корней характеристического уравнения.
. Его нет среди корней характеристического уравнения. 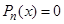 ;
; 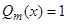 ;
; 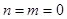 , следовательно
, следовательно 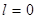 и значит, по формуле (21):
и значит, по формуле (21):
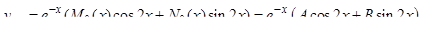 .
.
Для нахождения 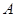 и
и 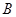 подставим
подставим 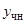 в исходное уравнение
в исходное уравнение  .
.

| 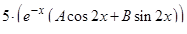
|

| 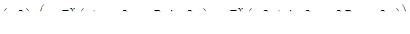
|
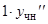
| 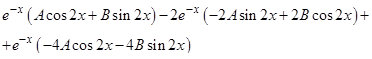
|
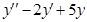
| 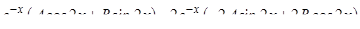 + +
 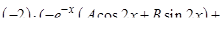
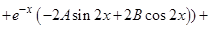 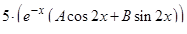
|
Просуммированные строки приравниваем к правой части 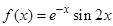 . Сократим выражение на
. Сократим выражение на 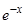 и упростим, затем приравниваем коэффициенты при одинаковых функциях:
и упростим, затем приравниваем коэффициенты при одинаковых функциях:
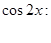
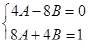 .
.
Решаем систему и находим 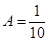 ;
; 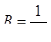 , следовательно,
, следовательно,
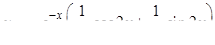 .
.
Запишем общее решение уравнения
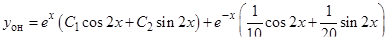 .
.
Пример 9. Для предложенных дифференциальных уравнений составить вид частного решения (коэффициенты находить не надо):
1) 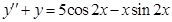 ;
;
2) 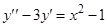 ;
;
3) 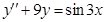 , 4)
, 4)  .
.
Решение.
1) 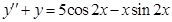 . Составим соответствующее однородное уравнение
. Составим соответствующее однородное уравнение 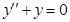 . Его характеристическое уравнение
. Его характеристическое уравнение 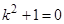 имеет корни
имеет корни 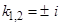 . Правая часть имеет вид
. Правая часть имеет вид 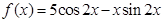 . Так как
. Так как 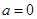 ,
, 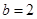 , то контрольное число
, то контрольное число 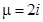 не совпадает с корнями характеристического уравнения. Многочлен
не совпадает с корнями характеристического уравнения. Многочлен 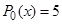 ,
, 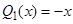 , поэтому
, поэтому 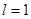 . Согласно формуле (21), частное решение имеет вид:
. Согласно формуле (21), частное решение имеет вид:
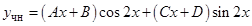 .
.
2) 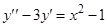 . Составим соответствующее однородное уравнение
. Составим соответствующее однородное уравнение 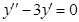 . Его характеристическое уравнение
. Его характеристическое уравнение 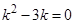 имеет корни
имеет корни  ,
,  . Правая часть имеет вид
. Правая часть имеет вид  . Следовательно
. Следовательно 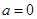 ,
, 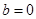 , контрольное число
, контрольное число 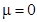 совпадает с одним из корней характеристического уравнения. Многочлен
совпадает с одним из корней характеристического уравнения. Многочлен 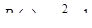 , поэтому
, поэтому 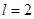 . Согласно формуле (22), частное решение имеет вид:
. Согласно формуле (22), частное решение имеет вид:
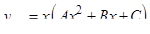 .
.
3) 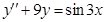 . Соответствующее однородное уравнение
. Соответствующее однородное уравнение 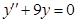 . Его характеристическое уравнение
. Его характеристическое уравнение 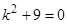 имеет корни
имеет корни 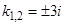 . Правая часть имеет вид
. Правая часть имеет вид 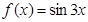 . Так как
. Так как 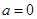 ,
, 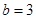 , то контрольное число
, то контрольное число  совпадает с одним корнем характеристического уравнения.
совпадает с одним корнем характеристического уравнения. 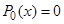 ,
, 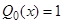 , следовательно
, следовательно 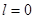 и согласно формуле (22), частное решение имеет вид:
и согласно формуле (22), частное решение имеет вид:
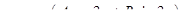 .
.
4)  . Составим соответствующее однородное уравнение.
. Составим соответствующее однородное уравнение. 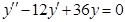 . Его характеристическое уравнение
. Его характеристическое уравнение 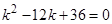 имеет корни,
имеет корни, 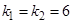 . Правая часть имеет вид
. Правая часть имеет вид  . Так как
. Так как 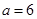 ,
, 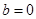 , то контрольное число
, то контрольное число 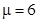 совпадает с корнями характеристического уравнения
совпадает с корнями характеристического уравнения 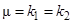 . Многочлен
. Многочлен 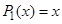 , поэтому
, поэтому 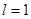 ,
, 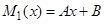 . Согласно формуле (23), частное решение имеет вид:
. Согласно формуле (23), частное решение имеет вид:
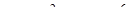 .
.
 2020-05-25
2020-05-25 410
410








