2020-05-25
357
Метод Лагранжа применяется для уравнений вида:
, (24)
причем правая часть 
может иметь любой вид. Общее решение уравнения (24) находят в виде: 
, (25), где 
и 
— неизвестные функции переменной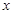 
, удовлетворяющие системе уравнений:
(26)
Функции 
и 
составляют фундаментальную систему решений соответствующего однородного уравнения 
.
Пример 10. Решить дифференциальные уравнения методом вариации произвольных постоянных (методом Лагранжа):
1) 
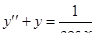; 2) 
.
Решение. 1) 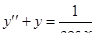. Находим общее решение соответствующего однородного уравнения 
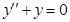. Характеристическое уравнение 
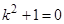имеет корни 
, следовательно, по табл. 1 
, 
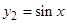. Общее решение неоднородного уравнения имеет вид: 
(*)
Функции 
являются решениями системы (26), которая в данном случае имеет вид:
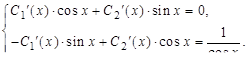Решаем ее методом Крамера:
; 
, 
, 
.
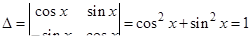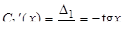Интегрируя, полученные выражения, находим :
;
.
Найденные подставляем в формулу (*). Получим общее решение неоднородного дифференциального уравнения:
|
|
|
.
2) . Находим общее решение соответствующего однородного уравнения 
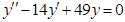. Характеристическое уравнение 
имеет корни 
, следовательно, по табл. 1 
, 
. Общее решение неоднородного уравнения будет иметь вид: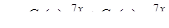 
. (**)
Функции являются решениями системы (26), которая в данном случае имеет вид: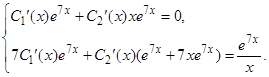 
Каждое из уравнений системы можно сократить на 
, получим:
Решаем систему методом Крамера: 
; 
, 
; 
; 
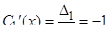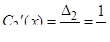.Интегрируя, полученные выражения, находим : 
; 
.
Найденные подставляем в формулу (**). Получим общее решение неоднородного дифференциального уравнения:
уравнения.
Контрольные вопросы по разделу «Дифференциальные уравнения»
1. Дифференциальные уравнения. Основные определения
3. Дифференциальные уравнения с разделяющимися переменными.
4. Однородные дифференциальные уравнения 1-го порядка
5. Линейные дифференциальные уравнения 1-го порядка
6. Линейные однородные дифференциальные уравнения 2-го порядка
7. Линейные неоднородные дифференциальные уравнения 2-го порядка
8. Метод неопределенных коэффициентов. Метод Лагранжа.
