2020-05-25
116
Задание 1. А. Доказать, что функция 
является решением дифференциального уравнения 
. Б. Выяснить, при каком значении параметра 
функция 
является решением дифференциального уравнения 
.
Задание 2. Найти общее решение дифференциального уравнения первого порядка 
, построить несколько интегральных кривых. Найти частное решение, удовлетворяющее начальным условиям: 
при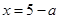 
.
| № варианта | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| a | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| b | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
Задание 3. Найти общее решение линейного дифференциального уравнения первого порядка:
1.  ;
| 2.  ;
|
3.  ;
| 4.  ;
|
5  .;
| 6.  ;
|
7.  ;
| 8.  ;
|
9.  ;
| 10.  .
|
Задание 4. Найти частное решение линейного однородного дифференциального уравнения второго порядка 
, удовлетворяющее начальным условиям: 
, 
.
Задание 5. Найти общее решение линейного неоднородного дифференциального уравнения второго порядка.
1. 
| 2. 
|
3. 
| 4. 
|
5. 
| 6.  ;
|
7.  ;
| 8.  ;
|
9.  ;
| 10. 
|
8. Образец теста по темам, пройденным в семестре.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО МОРСКОГО И РЕЧНОГО ТРАНСПОРТА
|
|
|
