Возмущенный режим работы СМ

Переходное сопротивление. Определяет сопротивление СМ без успокоительных обмоток в начальный момент короткого замыкания или другого возмущения.

Уравнения (2.49), (2.51) без учета активного сопротивления, трансформаторных эдс и эдс скольжения статорной обмотки в этом случае будут иметь следующий вид.

(3.4)

(3.4, б)

(3.4, а)

                  

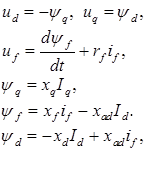
В начальный момент короткого замыкания t ₊ потокосцепление обмотки возбуждения скачком измениться не может в силу закона коммутации, поэтому третье уравнение из системы (3.4) можно исключить. Запишем при этих условиях отдельно уравнения СМ по оси d – (3.4, а) и по оси q – (3.4, б).

Найдем из системы (3.4,а) выражение для напряжения u_q:

(3.5)

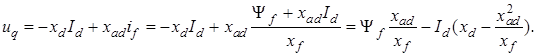
Выражение (3.5) можно представить в виде:

(3.6)

где   

 

Параметр  называют переходным сопротивлением синхронной машины, а  – переходной эдс.

Переходное сопротивление  представляет собой результирующую реактивность статорной обмотки в начальный момент возмущенного режима СМ при закороченной обмотке возбуждения. Переходная эдс , определяемая потокосцеплением обмотки возбуждения, в момент нарушения режима остается постоянной величиной в силу закона коммутации. Переходное сопротивление  и переходная эдс  позволяют связать установившийся режим с переходным, вызванным возмущением.

Преобразуем выражение для переходного сопротивления , учитывая, что x_d = x_ad + x_la, x_f = x_ad + x_lf:

(3.7)

.

(3.8)

Уравнение, аналогичное уравнению (3.6) для поперечного контура, получим, разрешив систему (3.4,б):

,                  

то есть в поперечной оси переходное сопротивление равно синхронному.

Сверхпереходное сопротивление. Определяет сопротивление СМ с демпферными контурами, а также в СМ с неявнополюсным ротором в начальный момент короткого замыкания или другого возмущения.

Уравнения (3.49), (3.51) без учета трансформаторных эдс и эдс скольжения, активного сопротивления r_a, активных сопротивлений демпферных контуров и при постоянстве потокосцепления обмотки возбуждения в момент нарушения режима будет иметь следующий вид.

(3.13) (3.14) (3.15) (3.15)

(3.10) (3.11) (3.12)

Продольная  ось

(3.9)

                  

Поперечная  ось

                  

Из уравнений (3.11), (3.12) и (3.15) выразим токи :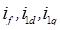

Подставляя эти выражения в (3.10), (3.14), после преобразований       получим:

Полученные выражения для потокосцеплений ψ_q и ψ_d можно представить в следующем виде:

 

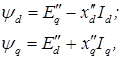
где ,  – с верхпереходные эдс в продольной и поперечной осях;     , – сверхпереходное сопротивление.

Введем индуктивные сопротивления рассеяния обмоток в выражение для :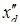

и окончательно получим

(3.18)

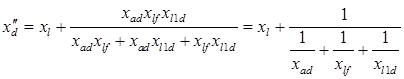
Выполним аналогичные преобразования для :

(3.19)

              

Рис. 3.1. Схемы для определения индуктивных сопротивлений СМ в продольной – а и поперечной – б осях

Сопротивления СМ можно представить в виде схем, позволяющих легко получить все приведенные выше формулы, как это показано       на рис. 3.1.