2020-05-21
110
Определение неявной функции. Дифференцирование неявной функции. Дифференцирование функций, заданных параметрически.
Цели занятия:
Должен уметь: Находить производные от неявных функций и заданных параметрически.
Должен знать: Определение неявной функции. Дифференцирование неявной функции. Дифференцирование функций, заданных параметрически.
Дифференциал функции.
Если функция 
имеет конечную производную в точке х, то полное приращение функции можно записать в виде
где a ®0, при D х ®0.
Дифференциалом функции в точке х называется главная, линейная относительно D х, часть полного приращения функции и обозначается 
или 
.
Из определения следует, что 
или 
. Можно также записать: 
Свойства дифференциала.
Если 
, 
– функции, дифференцируемые в точке х, то непосредственно из определения дифференциала следуют следующие свойства:
11) 
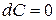, где 
12) 
13) 
14) 
15) 
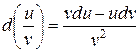
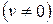
16) 
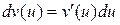
Производная функции, заданной параметрически.
Пусть 
.
Предположим, что эти функции имеют производные и функция 
имеет обратную функцию 
. Тогда функция 
может быть рассмотрена как сложная функция 
.
|
|
|
т.к. Ф (х) – обратная функция, то 
. Окончательно получаем:
Контрольные вопросы
1. Определение неявной функции.
2. Дифференцирование неявной функции.
3. Дифференцирование функций, заданных параметрически.
Тема 1.3. Приложения производной к задачам геометрии и механики.
Уравнение касательной к кривой. Нормаль к кривой. Уравнение нормали. Угол между двумя кривыми.
Цели занятия:
Должен уметь: составлять уравнение касательной и нормали; находить угол между двумя кривыми.
Должен знать: как составлять уравнение касательной и нормали; по какой формуле находить угол между двумя кривыми.
