2020-05-21
233
Оглавление
| Введение | 3 |
| Раздел 1. Дифференциальное исчисление функции одной переменной. | 4 |
| Тема 1.1. Дифференцирование явных функций. | 4 |
| Тема 1.2. Дифференцирование неявных функций. | |
| Тема 1.3. Приложения производной к задачам геометрии и механики. | |
| Тема 1.4. Производные высших порядков. Дифференциалы первого и высших порядков. | |
| Раздел 2.Дифференциальное исчисление функции многих переменных | |
| Тема 2.1. Полный дифференциал. | |
| Раздел 3. Неопределенный интеграл. | |
| Тема 3.1. Интегрирование по частям. | |
| Тема 3.2. Интегрирование рациональных дробей с помощью разложения на простейшие дроби. | |
| Раздел 4. Определенный интеграл. | |
| Тема 4.1. Вычисление площади плоской фигуры и поверхности вращения. | |
| Раздел 5. Численные методы решения прикладных задач | |
| Тема5.1.Приближенное решений уравнений. Интерполирование. | |
| Тема.5.2. Численное интегрирование дифференциальных уравнений. | |
| Список литературы |
Раздел 1. Дифференциальное исчисление функции одной
Переменной.
Тема 1.1. Дифференцирование явных функций.
Производная. Основные правила дифференцирования. Производные степени и корня. Производная сложной функции. Производные логарифмических, показательных и тригонометрических функций.
Цели занятия:
Должен уметь: вычислять производные функций.
Должен знать: определение производной функции; таблицу производных. Основные правила дифференцирования.
Производная функции.
Пусть x 1 и x 2 – значения аргумента, а 
и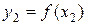 
– соответствующие значения функции 
. Разность 
называется приращением аргумента, а разность 
– приращением функции на отрезке 
Производной функции 
в точке 
называется предел отношения приращения функции в этой точке к приращению аргумента, когда последнее стремится к нулю.
Геометрический смысл.
Производная функции в точке x 0 равна угловому коэффициенту касательной к графику функции в точке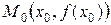 
, т.е. 
, где a – угол наклона касательной к графику функции в точке М 0.
Физический смысл.
Предположим, что функция 
описывает закон движения материальной точки по прямой линии, т.е. – путь, пройденный этой точкой от начала отсчета за время t. Тогда за время t 0 пройден путь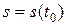 
, а за время t 1 – путь 
. За промежуток времени 
точка пройдет отрезок пути 
.
Отношение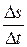 
выражает среднюю скорость движения материальной точки за время 
.
Предел отношения 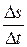при 
называется мгновенной скоростью движения материальной точки в момент времени t 0. Поскольку 
, то физический смысл производной функции – мгновенная скорость движения.
Соответственно, вторая производная функции – ускорение.
Основные правила дифференцирования.
Обозначим 
, 
и 
– функции, дифференцируемые в точке х.
1) 
, где С – постоянная величина.
2) 
3) 
4) 
5) 
6) 
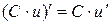
7) 
, если v ¹ 0
8) 
9) 
10) Если 
, , т.е. 
, то 
– производная сложной функции.
Таблица производных.
1) 
2) 
3) 
4) 
5) 
6) 
7) 
8) 
9) 
10) 
11) 
12) 
13) 
14) 
15) 
16) Пусть , , тогда 
Контрольные вопросы
1. Производная.
2. Основные правила дифференцирования.
3. Производные степени и корня.
4. Производная сложной функции.
5. Производные логарифмических, показательных и тригонометрических функций.
