Для функции 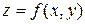 выражение
выражение 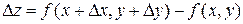 называется полным приращением.
называется полным приращением.
Функция 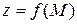 называется дифференцируемой в точке М, если ее полное приращение в этой точке может быть представлено в виде
называется дифференцируемой в точке М, если ее полное приращение в этой точке может быть представлено в виде 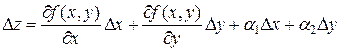 , где a 1 и a 2 – бесконечно малые функции при D х ® 0 и D у ® 0 соответственно.
, где a 1 и a 2 – бесконечно малые функции при D х ® 0 и D у ® 0 соответственно.
Полным дифференциалом функции 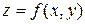 называется главная часть полного приращения функции D z, линейная относительно D х и D у, то есть
называется главная часть полного приращения функции D z, линейная относительно D х и D у, то есть
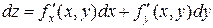
или
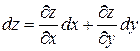
Для функции трех переменных 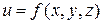 полный дифференциал находится по формуле:
полный дифференциал находится по формуле:
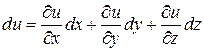
Производные сложных функций.
Пусть 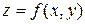 – функция двух переменных x и y, каждая из которых, в свою очередь, является функцией независимой переменной t:
– функция двух переменных x и y, каждая из которых, в свою очередь, является функцией независимой переменной t: 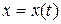 ,
, 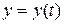 . Тогда функция
. Тогда функция 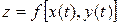 является сложной функцией независимой переменной t, а переменные x и y – промежуточные переменные.
является сложной функцией независимой переменной t, а переменные x и y – промежуточные переменные.
Теорема1. Если функции 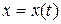 и
и 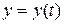 дифференцируемы в точке t, а функция
дифференцируемы в точке t, а функция 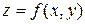 дифференцируема в точке
дифференцируема в точке 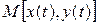 , то сложная функция
, то сложная функция 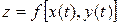 также дифференцируема в точке t. При этом производная сложной функции вычисляется по формуле:
также дифференцируема в точке t. При этом производная сложной функции вычисляется по формуле:
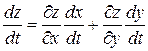
Если 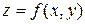 , где
, где 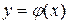 , то
, то 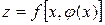 – сложная функция. Ее производная вычисляется по формуле:
– сложная функция. Ее производная вычисляется по формуле:
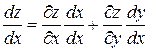 или
или 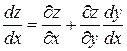
Пусть 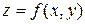 , где
, где 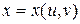 ,
, 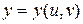 . Тогда, если функции
. Тогда, если функции 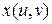 и
и 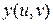 дифференцируемы в точке
дифференцируемы в точке 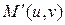 , а функция
, а функция 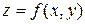 дифференцируема в точке
дифференцируема в точке 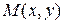 , то сложная функция
, то сложная функция 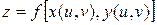 дифференцируема в точке
дифференцируема в точке 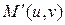 , причем ее частные производные вычисляются по формулам:
, причем ее частные производные вычисляются по формулам:
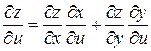 ,
, 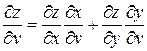
 2020-05-21
2020-05-21 158
158








