Уравнения касательной и нормали

Если функция  в точке x₀ имеет конечную производную, то

уравнение касательной имеет вид: ,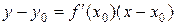

а уравнение нормали: .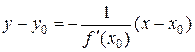

Направление кривой в каждой ее точке определяется направлением касательной к ней в этой точке, поэтому для нахождения угла наклона кривой в данной точке необходимо вычислить угол между касательной и осью Ox.

Углом между пересекающимися прямой и кривой называется угол между прямой и касательной к кривой, проведенной в точке их пересечения.

Углом между двумя пересекающимися кривыми называется угол между касательными к этим кривым, проведенным в точке их пересечения. Он находится по формуле:

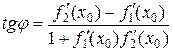
Контрольные вопросы

1. Уравнение касательной к кривой.

2.  Нормаль к кривой. Уравнение нормали.

3. Угол между двумя кривыми.

 

Тема 1.4. Производные высших порядков. Дифференциалы первого и высших порядков.

Производная высших порядков. Производная высших порядков от функций, заданных

параметрически. Определение и свойства дифференциала. Дифференциалы высших порядков.

Цели занятия:

Должен уметь: Вычисление производных и дифференциала высших порядков.

Должен знать: Определение и свойства дифференциала. Производная высших порядков от функций, заданных параметрически.

Производные и дифференциалы высших порядков.

Пусть функция  – дифференцируема на некотором интервале. Тогда, дифференцируя ее, получаем первую производную

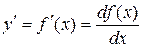
Если найти производную от функции , получим вторую производную функции .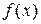

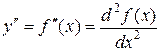
т.е.  или .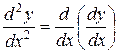

Этот процесс можно продолжить и далее, находя производные степени n.

.

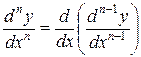Контрольные вопросы

1. Производная высших порядков.

2. Производная высших порядков от функций, заданных параметрически.

3. Определение и свойства дифференциала

4.  Дифференциалы высших порядков.

Раздел 2.Дифференциальное исчисление функции многих

Переменных