Тема 2.1. Полный дифференциал

Частные производные первого порядка. Полное приращение функции. Полный дифференциал функции. Частные производные и дифференциалы высших порядков. Дифференцирование сложных функций. Градиент функции.

Цели занятия:

Должен уметь: вычислять частные производные функции; находить дифференциалы и градиент функции.

Должен знать: Частные производные первого порядка. Полное приращение функции. Полный дифференциал функции. Частные производные и дифференциалы высших порядков. Дифференцирование сложных функций. Градиент функции.

Функции двух переменных.

Если любой паре упорядоченных чисел  из некоторого множества D поставлено в соответствие единственное число z, то переменная z называется функцией двух переменных.

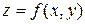
Переменную z называют зависимой переменной, а переменные x и y – независимыми. Множество D называется областью определения функции, а множество z – множеством значений функции.

Поскольку любую пару чисел  можно рассматривать как пару координат точки M на плоскости, то вместо 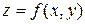 можно писать .

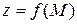Функция двух переменных изображается в пространстве в виде поверхности.

Частные приращения и частные производные.

Пусть в некоторой области задана функция 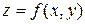. Возьмем произвольную точку  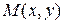и зададим приращение D х к переменной х, оставляя значение переменной y неизменным. Тогда величина  называется частным приращением функции по х.

Если существует предел , то он называется частной производной функции 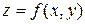 по переменной х и обозначается одним из следующих символов:

Аналогично определяется частная производная функции по у, то есть  – частное приращение функции по y. А предел  называется частной производной функции 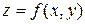 по переменной y и обозначается одним из следующих символов: