2020-05-21
321
Вспомним формулу производной произведения:
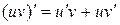
где u и v – некоторые функции от х. В дифференциальной форме:
Проинтегрировав, получаем: 
, а в соответствии с приведенными выше свойствами неопределенного интеграла:
или 
;
Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.
При использовании метода по частям за u берется такая функция, которая при дифференцировании упрощается, а за dv – та часть подынтегрального выражения, интеграл от которой известен или может быть найден.
Большую часть интегралов, вычисляемых по частям, можно разбить на три группы:
1. Интегралы вида 
, 
, 
, 
, 
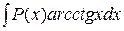, где P (x) – многочлен. Для их вычисления следует за u принимать одну из вышеуказанных функций, а dv = P (x) dx.
2. Интегралы вида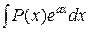 
, 
, 
, где P (x) – многочлен, а a – некоторое число. Для их вычисления следует приять u = P (x), а dv = eaxdx, dv = sin axdx, dv = cos axdx.
Как видно, последовательное применение формулы интегрирования по частям позволяет постепенно упростить функцию и привести интеграл к табличному.
|
|
|
3. Интегралы вида 
, 
, где a и b – некоторые числа. Эти интегралы вычисляются двукратным интегрированием по частям.
Контрольные вопросы
1. Свойства неопределенного интеграла.
2. Таблица основных интегралов.
3. Метод интегрирования по частям.
Тема 3.2. Интегрирование рациональных дробей с помощью разложения на простейшие
Дроби.
Интегрирование рациональных дробей с помощью разложения на простейшие дроби.
Цели занятия:
Должен уметь: Находить интегралы методом неопределенных коэффициентов.
Должен знать: Интегрирование рациональных дробей с помощью разложения на простейшие дроби.
