Пусть функция 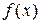 определена на отрезке
определена на отрезке  . Разобьем отрезок
. Разобьем отрезок  на n произвольных частей точками
на n произвольных частей точками  . На каждом из частичных отрезков выберем произвольно по одной точке:
. На каждом из частичных отрезков выберем произвольно по одной точке: 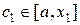 ,
,  , …,
, …,  .
.

Введем обозначения:  ,
,  , …,
, …,  .
.
Составим сумму:  , которая называется интегральной суммой функции
, которая называется интегральной суммой функции 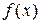 на отрезке
на отрезке  .
.
Геометрический смысл σ: Каждое слагаемое интегральной суммы представляет собой площадь прямоугольника с основанием  и высотой
и высотой  , покрытого штриховкой на рисунке.
, покрытого штриховкой на рисунке.
Обозначим через l = max(D xi), i = 1, 2, ¼, n – длину наибольшего частичного отрезка. Величину l иногда называют параметром разбиения.
Рассмотрим процесс, при котором число точек разбиения неограниченно возрастает таким образом, что величина l стремится к нулю.
Если существуетпредел интегральной суммы 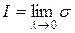 , то он называется определенным интегралом от функции
, то он называется определенным интегралом от функции  на отрезке
на отрезке 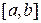 и обозначается
и обозначается

В этом случае функция  называется интегрируемой на отрезке
называется интегрируемой на отрезке 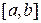 . Число a называется нижним пределом интегрирования, а число b – верхним пределом интегрирования.
. Число a называется нижним пределом интегрирования, а число b – верхним пределом интегрирования.
Если такой предел существует, то он не зависит от первоначального разбиения отрезка  и выбора точек ci. Из определения определенного интеграла следует, что его величина зависит только от вида функции
и выбора точек ci. Из определения определенного интеграла следует, что его величина зависит только от вида функции  и от чисел a и b. Следовательно, если заданы
и от чисел a и b. Следовательно, если заданы  и пределы интегрирования, то интеграл определяется однозначно и представляет собой некоторое число.
и пределы интегрирования, то интеграл определяется однозначно и представляет собой некоторое число.
|
|
Геометрический смысл определенного интеграла: Если  на отрезке
на отрезке 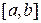 , то определенный интеграл
, то определенный интеграл  геометрически представляет собой площадь криволинейной трапеции – фигуры, ограниченной линиями
геометрически представляет собой площадь криволинейной трапеции – фигуры, ограниченной линиями 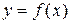 ,
,  ,
, 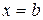 ,
, 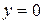 .
.
Если  на отрезке
на отрезке 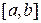 , то
, то  .
. 
Свойства определенного интеграла
1.  ;
;
2.  ;
;
3. Если  , то
, то  ;
;
4.  ;
;
5.  , где k – произвольное число.
, где k – произвольное число.
 2020-05-21
2020-05-21 152
152









