Функция 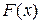 называется первообразной функцией функции
называется первообразной функцией функции 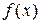 на отрезке
на отрезке 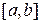 , если в любой точке этого отрезка верно равенство:
, если в любой точке этого отрезка верно равенство:
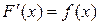 .
.
Надо отметить, что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число, т.е. 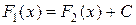 .
.
Неопределенным интегралом функции 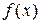 называется совокупность первообразных функций, которые определены соотношением:
называется совокупность первообразных функций, которые определены соотношением:
F (x) + C.
Записывают: 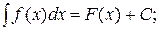 здесь
здесь 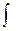 – знак интеграла,
– знак интеграла, 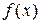 – подынтегральная функция,
– подынтегральная функция, 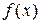 dx – подынтегральное выражение.
dx – подынтегральное выражение.
Вычисление неопределенного интеграла от заданной функции называется интегрированием.
Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке.
Интегральное исчисление широко применяется в физике, а также при решении различных технических задач. Основоположниками дифференциального и интегрального исчисления являются И. Ньютон и Г. Лейбниц.
Свойства неопределенных интегралов
1. Производная от неопределенного интеграла равна подынтегральной функции.
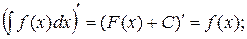
2. Дифференциал от неопределенного интеграла равен подынтегральному выражению.
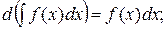
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого.
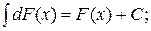
4. Интеграл от суммы или разности двух и более функций равен сумме или разности интегралов от этих функций
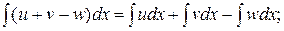
5. Постоянный множитель можно выносить за знак интеграла
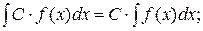
Таблица интегралов
| № | Интеграл | Значение | № | Интеграл | Значение |
| 1 | ò dx | x+C | 11 | 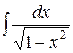
| 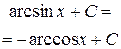
|
| 2 | 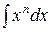
| 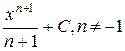
| 12 | 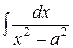
| 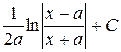
|
| 3 | 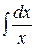
| 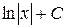
| 13 | 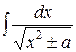
| 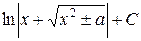
|
| 4 | 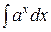
| 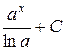
| 14 | 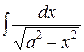
| 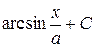
|
| 5 | 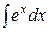
| 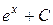
| 15 | 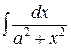
| 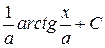
|
| 6 | 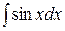
| – 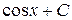
| 16 | 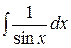
| 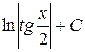
|
| 7 | 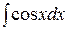
| 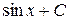
| 17 | 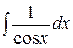
| 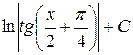
|
| 8 | 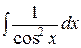
| 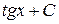
| 18 | 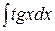
| 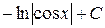
|
| 9 | 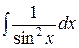
| 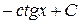
| 19 | 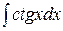
| 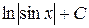
|
| 10 | 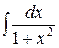
| 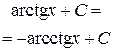
| 20 | 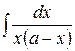
| 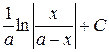
|
Способ подстановки (замены переменных).
Если требуется найти интеграл 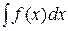 , но сложно отыскать первообразную, то иногда с помощью замены
, но сложно отыскать первообразную, то иногда с помощью замены 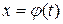 и
и 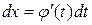 можно получить:
можно получить:
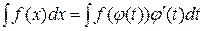
 2020-05-21
2020-05-21 157
157








