2020-05-21
81
Если функция 
непрерывна на отрезке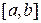 
и функция 
является ее первообразной на этом отрезке, то имеет место формула Ньютона-Лейбница
,
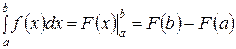то есть определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.
Замена переменных в определенном интеграле
Пусть задан интеграл 
, где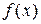 
– непрерывная функция на отрезке 
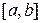. Введем новую переменную в соответствии с формулой 
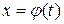. Тогда если:
1) 
, 
;
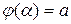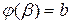2) 
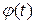и 
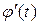непрерывны на отрезке 
;
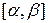3) 
определена на отрезке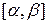 
,
то
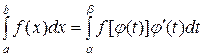
Эта формула называется формулой замены переменной в определенном интеграле.
Замечание. Если при вычислении неопределенного интеграла с помощью замены переменной следует от новой переменной t возвращаться к старой переменной x, то при вычислении определенного интеграла этого делать ненужно, т.к.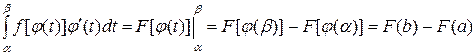 
Интегрирование по частям.
Если функци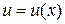и 
и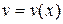 
непрерывны на отрезке 
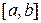, а также непрерывны на этом отрезке их производные, то справедлива формула:
которая называется формулой интегрирования по частям в определенном интеграле.
|
|
|
Также при вычислении определенного интеграла используются следующие правила:
Если 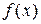– нечетная, то 
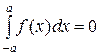, если нечетная,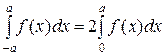 
Геометрические приложения определенного интеграла.
