а) Площадь криволинейной трапеции, ограниченной кривой 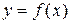 , прямыми
, прямыми 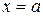 и
и 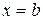 и отрезком
и отрезком 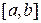 , вычисляется по формуле
, вычисляется по формуле 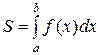
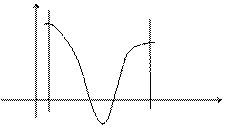
Если график расположен ниже оси Ох, т.е. 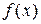 < 0, то площадь имеет знак “–“, если график расположен выше оси Ох, т.е.
< 0, то площадь имеет знак “–“, если график расположен выше оси Ох, т.е. 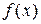 > 0, то площадь имеет знак “+”.
> 0, то площадь имеет знак “+”.
 у
у
+ +
0 a – b x
Таким образом, для нахождения суммарной площади используется формула 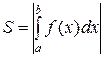 .
.
б) Площадь фигуры, ограниченной кривыми 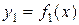 и
и 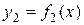
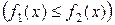 и прямыми
и прямыми 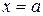 и
и 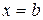 , находится по формуле
, находится по формуле 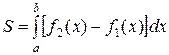
в) Если кривая задана параметрическими уравнениями 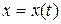 и
и 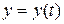 , то площадь криволинейной трапеции, ограниченной этой кривой, прямыми
, то площадь криволинейной трапеции, ограниченной этой кривой, прямыми 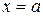 и
и 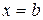 и отрезком
и отрезком 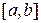 , выражается формулой
, выражается формулой 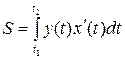 , где t 1 и t 2 определяются из уравнений
, где t 1 и t 2 определяются из уравнений 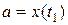 и
и 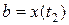 .
.
г) Для нахождения площади криволинейного сектора введем полярную систему координат. Уравнение кривой, ограничивающей сектор в этой системе координат, имеет вид 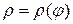 , где r – длина радиус-вектора, соединяющего полюс с произвольной точкой кривой, а j – угол наклона этого радиус-вектора к полярной оси.
, где r – длина радиус-вектора, соединяющего полюс с произвольной точкой кривой, а j – угол наклона этого радиус-вектора к полярной оси.
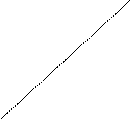 М
М
ρ
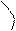
j
 0 l
0 l
Точка О называется полюсом, угол j – полярным углом, а луч l – полярнойосью. Можно установить связь между полярной системой координат и декартовой прямоугольной системой, если поместить начало декартовой прямоугольной системы в полюс, а полярную ось направить вдоль положительного направления оси Ох. Тогда координаты произвольной точки в двух различных системах координат связываются соотношениями:
x = ρcosj; y = ρsinj; x2 + y2 = ρ2
Площадь криволинейного сектора находится по формуле 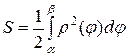 .
.
Длина дуги плоской кривой.
а) Если кривая 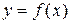 на отрезке
на отрезке 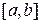 – гладкая, то есть
– гладкая, то есть 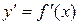 – непрерывна, то длина соответствующей дуги этой кривой находится по формуле
– непрерывна, то длина соответствующей дуги этой кривой находится по формуле 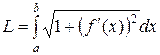
б) Если уравнение кривой задано параметрически, то длина дуги кривой, соответствующая монотонному изменению параметра t от t 1 до t 2, вычисляется по формуле 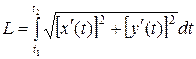
в) Если кривая задана в полярных координатах, то
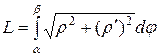
Объем тела.
а) Если площадь сечения тела плоскостью, перпендикулярной оси Ох может быть выражена как функция от x, то есть в виде 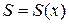 , то объем части тела, заключенной между перпендикулярными оси Ох плоскостями
, то объем части тела, заключенной между перпендикулярными оси Ох плоскостями 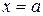 и
и 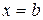 , находится по формуле:
, находится по формуле:
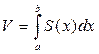
б) Если криволинейная трапеция, ограниченная кривой 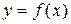 и прямыми
и прямыми 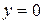 ,
, 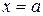 и
и 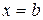 вращается вокруг оси Ох, то объем тела вращения вычисляется по формуле:
вращается вокруг оси Ох, то объем тела вращения вычисляется по формуле:
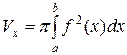
в) Если фигура, ограниченная кривыми 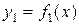 и
и 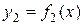 и прямыми
и прямыми 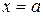 и
и 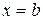 , вращается вокруг оси Ох, то объем тела вращения:
, вращается вокруг оси Ох, то объем тела вращения:
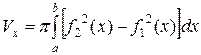
 2020-05-21
2020-05-21 115
115








