2020-05-21
144
Пусть действительный корень уравнения 
изолирован на отрезке 
. Возьмем на отрезке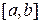 
такое число х 0, при котором 
имеет тот же знак, что и 
, т.е. 
(в частности, за х 0 может быть принят тот из концов отрезка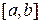 
, в котором соблюдено это условие). Проведем в точке 
касательную к кривой 
. За приближенное значение корня примем абсциссу точки пересечения этой касательной с осью Ох. Это приближенное значение корня находится по формуле
Применив этот прием вторично в точке 
, найдем
и т. д. Полученная таким образом последовательность 
имеет своим пределом искомый корень.
Геометрический смысл способа Ньютона заключается в 
том, что дуга кривой 
заменяется касательной к этой кривой. Поэтому способ Ньютона называют также способом касательных.
На рисунке изображено, как точки 
получаемые по способу Ньютона, приближаются к точке 
пересечения кривой 
с осью Ох.
