Метод половинного деления (дихотомии, бисекции, вилки, проб) отличается от большинства методов тем, что для его сходимости не требуется, чтобы функция f (x) была дифференцируемой, достаточно непрерывности f (x).
Пусть корень уравнения 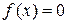 отделен, т.е. имеем, что f (a) и f (b) разных знаков: f (a)∙ f (b)<0, причем на отрезке
отделен, т.е. имеем, что f (a) и f (b) разных знаков: f (a)∙ f (b)<0, причем на отрезке 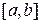 находится только один корень уравнения, функция f (x) непрерывна на
находится только один корень уравнения, функция f (x) непрерывна на 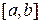 .
.
Алгоритм вычисления корня уравнения методом дихотомии:
1. Задать концы отрезка а и b, функцию f (x), точность e.
2. Разделить отрезок 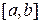 пополам точкой
пополам точкой 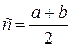 .
.
3. В качестве нового интервала изоляции принять ту половину интервала 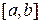 , на концах которой функция имеет разные знаки. Для этого:
, на концах которой функция имеет разные знаки. Для этого:
а) вычислить значение функции в точках a и с;
б) если F (a)· F (с)<0, то корень находится на интервале 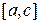 . Тогда
. Тогда
b = с. Если условие не выполняется, то корень находится на интервале
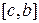 и a = с. В обоих случаях получаем новый интервал
и a = с. В обоих случаях получаем новый интервал 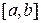 , длина которого в 2 раза меньше предыдущего интервала.
, длина которого в 2 раза меньше предыдущего интервала.
4. Итерационный процесс повторяется, начиная со второго пункта до тех пор, пока длина 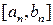 не станет равной или меньше e, то есть пока не выполнится условие
не станет равной или меньше e, то есть пока не выполнится условие 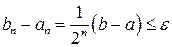 .
.
Получим последовательность отрезков 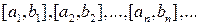 , на концах которых выполняется неравенство
, на концах которых выполняется неравенство 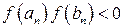 . Последовательность
. Последовательность 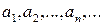 является монотонной неубывающей ограниченной последовательностью; а
является монотонной неубывающей ограниченной последовательностью; а 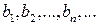 – монотонной невозрастающей ограниченной последовательностью. Следовательно, существует предел:
– монотонной невозрастающей ограниченной последовательностью. Следовательно, существует предел: 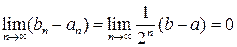 . Тогда
. Тогда 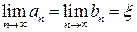 . Отсюда
. Отсюда 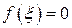 , т.е.
, т.е. 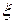 является корнем уравнения
является корнем уравнения 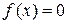 , причем
, причем 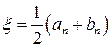 .
.

Метод половинного деления практически удобно применять для грубого нахождения приближенного корня данного уравнения, так как при увеличении точности значительно возрастает объем вычислительной работы.
Контрольные вопросы
1. Метод хорд.
2. Метод Касательных.
3. Метод итераций.
4. Интерполяционный многочлен Лагранжа.
Тема.5.2. Численное интегрирование дифференциальных уравнений.
Метод Эйлера. Метод Рунге – Кутта.
Цели занятия:
Должен уметь: Используя метод Эйлера и Рунге – Кутта находить значения функции.
Должен знать: Метод Эйлера. Метод Рунге – Кутта.
Метод Эйлера
Известно, что уравнение 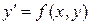 задает в некоторой области поле направлений. Решение этого уравнения с некоторыми начальными условиями дает кривую, которая касается поля направлений в любой точке.
задает в некоторой области поле направлений. Решение этого уравнения с некоторыми начальными условиями дает кривую, которая касается поля направлений в любой точке.
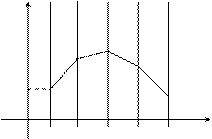
Если взять последовательность точек х 0, х 1, х 2, …. и заменить на получившихся отрезках интегральную кривую на отрезки касательных к ней, то получим ломаную линию.
 y
y
M 2
M 1 M 3
M 0
y 0 M 4
0 x 0 x 1 x 2 x 3 x 4 x
При подстановке заданных начальных условий (х 0, у 0) в дифференциальное уравнение  получаем угловой коэффициент касательной к интегральной кривой в начальной точке
получаем угловой коэффициент касательной к интегральной кривой в начальной точке
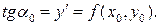
Заменив на отрезке [ x 0, x 1] интегральную кривую на касательную к ней, получаем значение
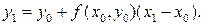
Производя аналогичную операцию для отрезка [ x 1, x 2], получаем:
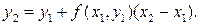
Продолжая подобные действия далее, получаем ломаную кривую, которая называется ломаной Эйлера.
Можно записать общую формулу вычислений:


Если последовательность точек хi выбрать так, чтобы они отстояли друг от друга на одинаковое расстояние h, называемое шагом вычисления, то получаем формулу:
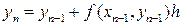 (19)
(19)
Следует отметить, что точность метода Эйлера относительно невысока. Увеличить точность можно, конечно, уменьшив шаг вычислений, однако, это приведет к усложнению расчетов. Поэтому на практике применяется так называемый уточненный метод Эйлера или формула пересчета.
Суть метода состоит в том, что в формуле 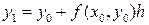 вместо значения
вместо значения 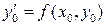 берется среднее арифметическое значений
берется среднее арифметическое значений 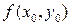 и
и 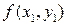 . Тогда уточненное значение:
. Тогда уточненное значение:
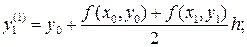
Затем находится значение производной в точке 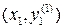 . Заменяя
. Заменяя  средним арифметическим значений
средним арифметическим значений 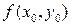 и
и 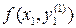 , находят второе уточненное значение у 1.
, находят второе уточненное значение у 1. 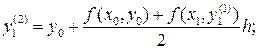 затем третье:
затем третье: 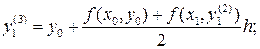 и т.д. пока два последовательных уточненных значения не совпадут в пределах заданной степени точности. Тогда это значение принимается за ординату точки М 1 ломаной Эйлера.
и т.д. пока два последовательных уточненных значения не совпадут в пределах заданной степени точности. Тогда это значение принимается за ординату точки М 1 ломаной Эйлера.
Аналогичная операция производится для остальных значений у.
Метод Рунге-Кутта
Метод Рунге-Кутта является более точным по сравнению с методом Эйлера.
Суть уточнения состоит в том, что искомое решение представляется в виде разложения в ряд Тейлора. 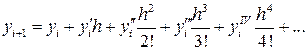
Если в этой формуле ограничиться двумя первыми слагаемыми, то получим формулу метода Эйлера. Метод Рунге-Кутта учитывает четыре первых члена разложения.
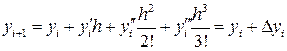 .
.
В методе Рунге-Кутта приращения D yi предлагается вычислять по формуле:
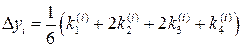
где коэффициенты ki вычисляются по формулам:
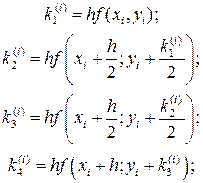
Контрольные вопросы
1. Метод Эйлера.
2. Метод Рунге - Кутта
 2020-05-21
2020-05-21 1593
1593