Предполагается, что при управлении используется информация только о времени, т.е. система является разомкнутой по состоянию и реализуется программное управление:
| УУ |
| ОУ |

|

|
Постановка задачи оптимального управления включает в себя:
- математическую модель ОУ в виде обыкновенного дифференциального уравнения первого порядка;
- цель управления (критерий оптимальности, количественно характеризующий качество управления), в виде функционала;
- различные ограничения на допустимые управления, допустимые траектории системы в пространстве состояний, длительность процесса управления и т.д.
Формальная постановка задачи нахождения оптимального управления
Заданы:
а). Математическая модель ОУ
 (1)
(1)
где: 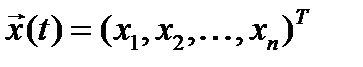 - вектор состояния системы,
- вектор состояния системы, 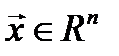 ;
;
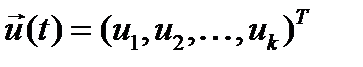 - вектор управления,
- вектор управления, 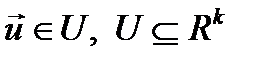 , U – заданное множество допустимых управлений;
, U – заданное множество допустимых управлений;
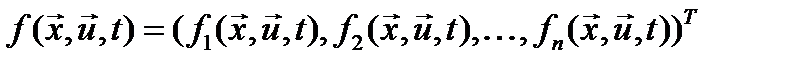 - непрерывная вместе со своими частными производными вектор-функция,
- непрерывная вместе со своими частными производными вектор-функция, 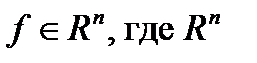 - n -мерное евклидово пространство.
- n -мерное евклидово пространство.
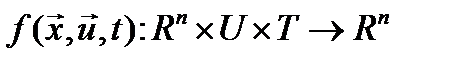
t – время, 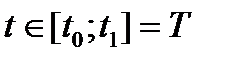 - интервал времени функционирования системы.
- интервал времени функционирования системы.
Момент начала процесса t 0 задан, а момент окончания процесса t 1 или задан, или определяется первым моментом достижения точкой 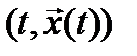 некоторой заданной гиперповерхности
некоторой заданной гиперповерхности 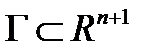 ,
,
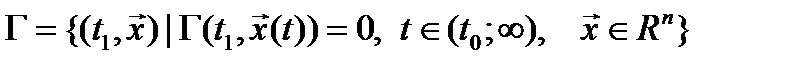 ,
,
т.е. в момент времени t 1 должно выполняться условие 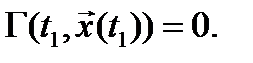
b). Функционал 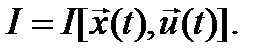
Требуется определить вектор функции 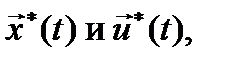 доставляющие минимум заданному функционалу при переводе системы из начального состояния
доставляющие минимум заданному функционалу при переводе системы из начального состояния 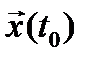 в конечное состояние
в конечное состояние 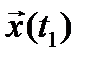 .
.
 2020-05-25
2020-05-25 213
213








