Ι – Вариант
1. ABCDA1B1C1D1 - параллелепипед. Изобразите на рисунке векторы, равные: а)  +
+  + +
+ +  1+
1+  ; б)
; б)  –
–  1.
1.
2. В тетраэдре ДАВС точка М-точка пересечения медиан грани ВДС, а точка Е-середина ребра АС. Разложите вектор  по векторам
по векторам  ;
;  и
и  .
.
3. Даны три неколлинеарных вектора 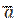 ;
;  и
и  . Найдите значение p и q, при которых векторы
. Найдите значение p и q, при которых векторы  =p
=p  +q
+q  +8
+8 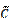 и
и  =
=  +p
+p  +q
+q 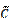 коллинеарны.
коллинеарны.
ΙΙ – Вариант
1. ABCDA1B1C1D1 - параллелепипед. Изобразите на рисунке векторы, равные: а)  +
+  + +
+ +  1+
1+  ; б)
; б) 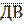 –
–  1.
1.
2. В тетраэдре ДАВС точка М-точка пересечения медиан грани АВС, а точка Е-середина ребра ДВ. Разложите вектор  по векторам
по векторам  ;
; 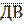 и
и  .
.
3. Даны три неколлинеарных вектора 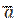 ;
;  и
и  . Найдите значение k, при которых векторы
. Найдите значение k, при которых векторы  =k
=k  +k2
+k2  +2
+2 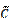 и
и  =
=  +k
+k  +
+ 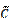 коллинеарны.
коллинеарны.
Ответы.
| Задание | Ι – Вариант | ΙΙ – Вариант |
| №1(а). | 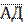 1. 1.
| 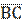 1. 1.
|
| №1(б). |  . .
|  . .
|
| №2. |  = =  – –  + + + + 
|  = =  – –  + + + + 
|
| №3. | p = 2; q = 4. | k = 2. |
| Критерии оценки: | ||
| №1(а). 4 балла | Разбалловка: | |
| №1(б). 3 балла | От 0 до 2 – оценка «Один», | |
| №2. 2 балла | От 3 до 5 – оценка «Два», | |
| №3. 4 балла | От 6 до 7 – оценка «Три», | |
| От 8 до 10– оценка «Четыре», | ||
| Итого: 13 баллов | От 11 до 13 – оценка «Пять». |
Тема 16. Метод координат в пространстве. Движения.
Ι – Вариант
1. Даны два вектора  (-2; 1; -1) и
(-2; 1; -1) и  (1; -3; 2). Найдите
(1; -3; 2). Найдите  и
и  +
+  .
.
2. Даны точки А(-1; 2; 1), В(3; 0; 1), С(2; -1; 0) и Д(2; 1; 2). Найдите:1) угол между векторами  и
и  ; 2) расстояние между серединами отрезков АВ и СД.
; 2) расстояние между серединами отрезков АВ и СД.
3. Даны две точки: А, лежащая в плоскости хОу, и В(1; 1; 1), причём абсцисса точки А равна её ординате. Прямая АВ составляет с плоскостью zOy угол в 300. Найдите координаты точки А.
ΙΙ – Вариант
1. Даны два вектора  (-2; 1; -1) и
(-2; 1; -1) и  (1; 3; 2). Найдите
(1; 3; 2). Найдите  и
и  .
.
2. Даны точки Е(1; -2; 2), F(3; 0; 2), K(0; -2; 3) и T(2; 4; 1). Найдите: 1) угол между векторами  и
и  ; 2) расстояние между серединами отрезков ЕF и КТ.
; 2) расстояние между серединами отрезков ЕF и КТ.
3. Даны две точки: М, лежащая в плоскости хОz, и Р(1; 2; 1), причём абсцисса точки М равна её аппликате. Прямая РМ составляет с плоскостью хOy угол в 300. Найдите координаты точки М.
Ответы.
| Задание | Ι – Вариант | ΙΙ – Вариант |
| №1. |  = =  ; ;  + +  = = 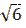 + +  . .
|  = =  ; ;  = =  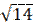 . .
|
| №2. | α =1800 – arccos  ; ;  = =  . .
| α = arccos  ; ;  = =  . .
|
| №3. | А(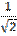 +1; +1;  +1; 0) или А( +1; 0) или А( +1; +1;  +1; 0). +1; 0).
| М( +1; 0; +1; 0;  +1) или М( +1) или М( ). ).
|
| Критерии оценки: | ||
| №1. 7 баллов | Разбалловка: | |
| №2. 2 балла | От 0 до 2 – оценка «Один», | |
| №3. 4 балла | От 3 до 5 – оценка «Два», | |
| От 6 до 7 – оценка «Три», | ||
| От 8 до 10– оценка «Четыре», | ||
| Итого: 13 баллов | От 11 до 13 – оценка «Пять». |
Тема 17. Интеграл.
Ι – Вариант
1. Найти первообразную для функции f(x) = х3+2, график которой проходит через точку М(2;15).
2. Вычислить интеграл:

3. Вычислить площадь фигуры, ограниченной линиями: у=х2+1, у=0, х=1, х=4.
4. Скорость движения тела изменяется по закону 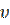 (t) = 3t + 4(м/с). Найдите перемещение тела через 2с после начала движения.
(t) = 3t + 4(м/с). Найдите перемещение тела через 2с после начала движения.
5. Вычислить интеграл:

ΙΙ – Вариант
1. Найти первообразную для функции f(x) = 4  х2, график которой проходит через точку М(-3;9).
х2, график которой проходит через точку М(-3;9).
2. Вычислить интеграл:

3. Вычислить площадь фигуры, ограниченной линиями: у = 9  х2, у = 0.
х2, у = 0.
4. Скорость движения тела изменяется по закону 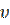 (t) = 3+2t (м/с). Найдите перемещение тела через 3с после начала движения.
(t) = 3+2t (м/с). Найдите перемещение тела через 3с после начала движения.
5. Вычислить интеграл:

Ответы.
| Задание | Ι – Вариант | ΙΙ – Вариант |
| №1. |  + 2х +7. + 2х +7.
| 4х –  + 12. + 12.
|
| №2. | 10  . .
| 1  . .
|
| №3. | 24. | 36. |
| №4. | 14м. | 18м. |
| №5. |  . .
|  . .
|
| Критерии оценки: | ||
| №1. 3 балла | Разбалловка: | |
| №2. 3 балла | От 0 до 3 – оценка «Один», | |
| №3. 3 балла | От 4 до 6 – оценка «Два», | |
| №4. 3 балла | От 7 до 9 – оценка «Три», | |
| №5. 4 баллов | От 10 до 12–оценка«Четыре», | |
| Итого: 16 баллов | От 13 до 16 – оценка «Пять». |
 2020-05-25
2020-05-25 193
193








