Ι – Вариант
1. Укажите случайные, достоверные и невозможные события, которые могут произойти в результате вытягивания одного экзаменационного билета из 25 предложенных.
2. Из 17 роз растущих на клумбе 9 белых, а остальные- красные. Какова вероятность того, что наугад выбранная роза, будет красной?
3. Найти моду, медиану и среднее значение выборки: 3;6;8;2;1;3;2;1;3;7.
4. В ящике находятся 3 белых и 5 черных шаров. Какова вероятность того, что из двух вынутых наугад шаров оба будут белыми?
ΙΙ – Вариант
1. Укажите случайные, достоверные и невозможные события, которые могут произойти в результате вытягивания из колоды двух игральных карт.
2. Из 24 стаканов, стоящих на столе, 18 были с компотом, а остальные с соком. Какова вероятность того, что наугад взятый стакан будет с соком?
3. Найти моду, медиану и среднее значение выборки: 4;6;5;2;7;2;3;8;1;9.
4. В ящике находятся 5 белых и 7 черных шаров. Какова вероятность того, что из двух вынутых наугад шаров оба будут черными?
Ответы.
| Задание | Ι – Вариант | ΙΙ – Вариант |
| №1. | С: вытянули билет любой до №25 включительно. Д: вытянули билет от №1 до №25. Н: вытянули билет после №25. | С: вытянули 2 разные по масти карты. Д: вытянули 2 разные карты от 6 до туза. Н: вытянули 2 одинаковые карты. |
| №2. | 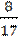 . .
|  . .
|
| №3. | Мо = 3; Ме = 3; 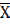 = 3,6. = 3,6.
| Мо = 2; Ме = 4,5; 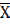 = 4,7. = 4,7.
|
| №4. | 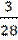 . .
| 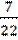 . .
|
| Критерии оценки: | ||
| №1. 6 балла | Разбалловка: | |
| №2. 3 балла | От 0 до 3 – оценка «Один», | |
| №3. 3 балла | От 4 до 6 – оценка «Два», | |
| №4. 4 балла | От 7 до 9 – оценка «Три», | |
| От 10 до 12–оценка«Четыре», | ||
| Итого: 16 баллов | От 13 до 16 – оценка «Пять». |
Контрольная работа за V семестр
I - Вариант
1. Решить уравнение: 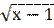 = х
= х  3.
3.
2. Найти максимумы и минимумы функции f(x) = –12х+х3.
3. В тетраэдре ДАВС точка М-точка пересечения медиан грани ВДС, а точка Е-середина ребра АС. Разложите вектор  по векторам
по векторам 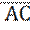 ;
; 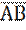 и
и  .
.
4. Объём цилиндра равен 96π см3. Найти длину диагонали осевого сечения цилиндра, если его высота равна 6 см.
5. Найти вероятность того, что наугад выбранное двузначное число не будет кратным 25.
II - Вариант
1. Решить уравнение:  = х+1.
= х+1.
2. Найти максимумы и минимумы функции f(x) = 3х–х3.
3. В тетраэдре ДАВС точка М-точка пересечения медиан грани АВС, а точка Е-середина ребра ДВ. Разложите вектор  по векторам
по векторам  ;
;  и
и 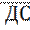 .
.
4. Объём цилиндра равен 175π см3. Найти длину окружности основания цилиндра, если его высота равна 7 см.
5. В ящике лежат 12 красных, 13 синих и 7 зелёных карандашей. Наугад вынимают один карандаш. Какова вероятность того, что он будет не зелёного цвета?
Ответы.
| Задание | Ι – Вариант | ΙΙ – Вариант |
| №1. | 5. | 1. |
| №2. | fmax =16, fmin = –16. | fmax=2, fmin = –2. |
| №3. |  = = 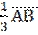 -- --  + + + + 
|  = =  -- --  + + + + 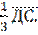
|
| №4. | 10см. | 10π см. |
| №5. |  . .
|  . .
|
| Критерии оценки: | ||
| №1. 3 балла | Разбалловка: | |
| №2. 3 балла | От 0 до 3 – оценка «Один», | |
| №3. 3 балла | От 4 до 6 – оценка «Два», | |
| №4. 3 балла | От 7 до 9 – оценка «Три», | |
| №5. 4 баллов | От 10 до 12–оценка«Четыре», | |
| Итого: 16 баллов | От 13 до 16 – оценка «Пять». |
 2020-05-25
2020-05-25 186
186








