Тема: Вычисление определенного интеграла различными методами.
Цель: Закрепление навыков и умений вычисления определённого интеграла.
Задание №1 Найти неопределенные интегралы.
| Метод интегрирования | Вариант | ||
| 1 | 2 | 3 | |
| Непосредственное интегрирование | 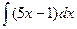

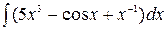

| 



| 
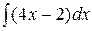


|
| Метод подстановки | 



| 



| 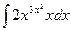



|
| Интегрирование по частям | 
| 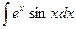
| 
|
Практическая работа № 12
Тема: Вычисление площадей и объемов с применением определенного интеграла.
Цель: применить формулу определенного интеграла для нахождения площади фигуры и объема тела.
Задание №1 Вычислить площадь фигуры ограниченной кривой y=f(x) и прямыми х1=а и х2=b.
| Вариант | Дано |
| 1 | у=5х; у=0; х=2 |
| 2 | 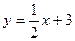 ; у=0; на отрезке (-2;4) ; у=0; на отрезке (-2;4)
|
| 3 | у=х2+2; у=0; х=-1; х=2 |
| 4 | y=sin x на 
|
Задание №2 Вычислить площадь фигуры, ограниченной параболой у=ах2+bх+с и прямой у=kх+b. Сделать чертеж
| Вариант | Дано |
| 1 | у = -х2 + 4х - 1; у = -х - 1. |
| 2 | у = х2 - 6х + 7; у = х + 1 |
| 3 | у = -х2 + 6х -5; у = х - 5 |
| 4 | у = х2 - 6х + 7; у = -х + 7 |
Задание №3 Вычислить объем тела, ограниченной кривой y=f(x) и прямыми х1=а и х2=b.
| Вариант | Дано |
| 1 | y=x  +1, y=0, x=0, x=1 +1, y=0, x=0, x=1
|
| 2 | y=4x-x  , y=0 , y=0
|
| 3 | y=x  -4x, y=0, x=- -4x, y=0, x=-  , x=- , x=- 
|
| 4 | y=  , x=1, x=3, y=0 , x=1, x=3, y=0
|
Практическая работа № 13.
Тема: Решение дифференциальных уравнений с разделяющимися переменными.
Цель: Выработать навыки и умения по решению дифференциальных уравнений первого порядка, по нахождению их общего и частного решений
Вариант 1
1.Найти общее решение дифференциального уравнения
а) (х + 1)ydx = dy.
б) 
в) 
г) 
2. Решить задачу Коши:
а) 
 , при f(0)=1
, при f(0)=1
б)  , при f(5)=2
, при f(5)=2
в) 
Вариант 2
1.Найти общее решение дифференциального уравнения:
а) 2xdx = 3y2dy
б) 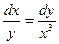
в) 
г) 
2.Найти решение задачи Коши:
а)  , при f(0)=1
, при f(0)=1
б)  , при f(0)=4
, при f(0)=4
в) 
Практическая работа № 14.
Тема: О днородных дифференциальных уравнений первого порядка.
Цель: Научиться решать дифференциальные уравнения первого порядка
Вариант 1
1. Найти общее решение дифференциального уравнения
А) xy’=3y-x
Б) 
2. Найти частное решение дифференциального уравнения, удовлетворяющий указанным начальным условиям:
 , y(1)=2
, y(1)=2
Вариант 2
1. Найти общее решение дифференциального уравнения
А) (x-y)dx + xdy = 0
Б) xy’ – xcos2(y/x)=y
2. Найти частное решение дифференциального уравнения, удовлетворяющий указанным начальным условиям:
y2 +x2y’ = 0, y(1)=1
Вариант 3
1. Найти общее решение дифференциального уравнения
А) 
Б) 
2. Найти частное решение дифференциального уравнения, удовлетворяющий указанным начальным условиям:
 , y(1)=1
, y(1)=1
 2020-05-25
2020-05-25 285
285








