Тема: «Показательная и тригонометрическая формы записи комплексных чисел. Действия над комплексными числами, заданными в тригонометрической и показательной формах.»
Цель: выполнять действия над комплексными числами в тригонометрической и показательной формах.
Вариант 1
1. На комплексной плоскости построить точки:
1) 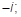 2)
2) 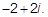
2. Выполнить действия:
1) 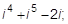 2)
2) 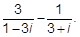
3. Решить уравнение 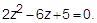
4. Дано комплексное число 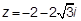 . Записать его в тригонометрической форме.
. Записать его в тригонометрической форме.
5. Возвести в степень 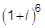 в показательной форме.
в показательной форме.
6. Решить уравнение 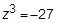 , пользуясь формулой Муавра.
, пользуясь формулой Муавра.
Вариант 2
1. На комплексной плоскости построить точки:
1) 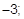 2)
2) 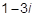 .
.
2. Выполнить действия:
1) 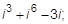 2)
2) 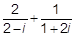 .
.
3. Решить уравнение 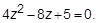
4. Дано комплексное число 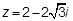 . Записать его в тригонометрической форме.
. Записать его в тригонометрической форме.
5. Возвести в степень 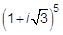 в показательной форме.
в показательной форме.
6. Решить уравнение 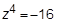 , пользуясь формулой Муавра.
, пользуясь формулой Муавра.
ПРАКТИЧЕСКАЯ РАБОТА № 3 «Матрицы и действия над ними. Определители и их вычисление»
Цель практической работы: освоить способы выполнения операций над матрицами, элементарные преобразования матриц, вычисление определителя, нахождение обратной матрицы.
ВАРИАНТ 1
1) Дано: A,B, С. Найти: а) 3А; б) (2А-3В)С; в) detА
2) Дано: A,B. Найти: а) 3A+B; б) AB; в) А-1двумя способами
| Вариант | Дано к заданию 1 | Дано к заданию 2 |
| 1 | 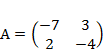 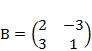
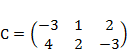
| 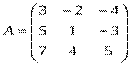 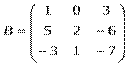
|
| 2 | 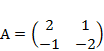 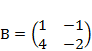
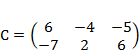
| 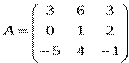 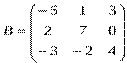
|
| 3 | 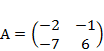 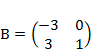
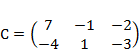
| 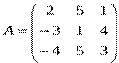 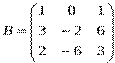
|
| 4 | 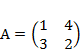 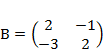
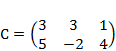
| 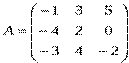 
|
Практическая работа № 4
Тема: Решений систем линейных уравнений методом Крамера.
Цель: Применение формул Крамера, метода Гаусса и матричного метода к решению систем линейных уравнений.
Вариант
1. Решить по формулам Крамера следующую систему уравнения:
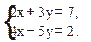
2. Решить по формулам Крамера, методом Гаусса и матричным методом следующую систему уравнения:
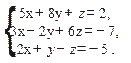
Вариант
1. Решить по формулам Крамера следующую систему уравнения:
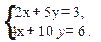
2.. Решить по формулам Крамера, методом Гаусса и матричным методом следующую систему уравнения:
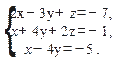
Вариант
1. Решить по формулам Крамера следующую систему уравнения:
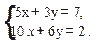
2.. Решить по формулам Крамера, методом Гаусса и матричным методом следующую систему уравнения:
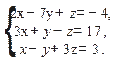
 2020-05-25
2020-05-25 433
433








