Работа силы электрического поля по переносу положительного заряда от одной точки цепи к другой (работа тока  ) за время t и мощность тока (мощность устройства, через которое протекает ток)
) за время t и мощность тока (мощность устройства, через которое протекает ток)  определяются по формулам (при постоянном токе):
определяются по формулам (при постоянном токе):
 (16)
(16)
 (17)
(17)
где 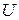 – напряжение между точками;
– напряжение между точками;  – сила тока на участке цепи, по которому переносится заряд.
– сила тока на участке цепи, по которому переносится заряд.
Работа тока A за время t по переносу положительного заряда от точки с большим потенциалом  к точке с меньшим потенциалом
к точке с меньшим потенциалом  и мощность тока P определяются
и мощность тока P определяются
1) для однородного участка цепи по формулам:
 (18)
(18)
 (19)
(19)
2) для неоднородного участка цепи – по формулам:
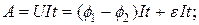 (20)
(20)
 (21)
(21)
3) для замкнутой цепи – по формулам:
 (22)
(22)
 (23)
(23)
 3.1.2. Примеры решения задач
3.1.2. Примеры решения задач
З а д а ч а 11. Мощность автомобильного стартера 5,9 кВт. Найти работу тока за 10 с во время запуска двигателя.
Дано:
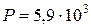 Вт; Вт;
 с.
Найти: с.
Найти: 
| Решение.
Согласно формуле (16) работа тока 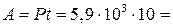 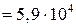 Дж.
Ответ: Дж.
Ответ:  Дж. Дж.
|
З а д а ч а 12. При ремонте электрической плитки ее спираль укоротили на 20 %. Во сколько раз изменилась при этом мощность плитки?
Дано:
 Найти:
Найти: 
| Решение.
Определим мощность плитки по формуле (19):  а сопротивление спирали – по формуле (2): а сопротивление спирали – по формуле (2): 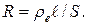 Объединив эти формулы, получим: Объединив эти формулы, получим:
|
 откуда
откуда  и
и  (при изменении сопротивления спирали напряжение на клеммах источника питания не меняется). Используя условие
(при изменении сопротивления спирали напряжение на клеммах источника питания не меняется). Используя условие  , найдем отношение мощностей плитки до и после ремонта:
, найдем отношение мощностей плитки до и после ремонта: 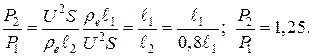
Ответ: 
З а д а ч а 13. ЭДС батареи 24 B. Наибольшая сила тока, которую может обеспечить батарея, 10 А. Найти наибольшую мощность, которая может выделяться во внешней цепи.
Дано:
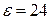 В; В;
 А.
Найти: А.
Найти: 
| Решение.
Согласно формуле (19) мощность во внешней цепи
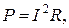 (24)
где (24)
где  – сила тока; – сила тока;  – полное сопротивление внешней цепи. – полное сопротивление внешней цепи.
|
Согласно закону Ома (12) для полной цепи
 - (25)
- (25)
наибольшая сила тока, которую может обеспечить батарея, – это сила тока, соответствующая минимально возможному сопротивлению внешней цепи ( ), – сила тока короткого замыкания. Поэтому
), – сила тока короткого замыкания. Поэтому  , откуда внутреннее сопротивление источника
, откуда внутреннее сопротивление источника
 (26)
(26)
Подставив уравнение (25) в выражение (24), получим:
 (27)
(27)
Максимуму мощности (как функции 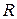 ) соответствует равенство нулю производной:
) соответствует равенство нулю производной:  Следовательно, значение сопротивления
Следовательно, значение сопротивления 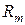 , при котором мощность максимальна, найдем, приравняв к нулю эту производную:
, при котором мощность максимальна, найдем, приравняв к нулю эту производную:  Отсюда следует, что
Отсюда следует, что  Таким образом,
Таким образом, 
Подставив значение  в формулу (27) и учитывая соотношение (26), получим:
в формулу (27) и учитывая соотношение (26), получим:  Численный расчет дает:
Численный расчет дает: 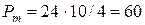 Вт.
Вт.
Ответ:  Вт.
Вт.
Закон Джоуля – Ленца
 2020-05-21
2020-05-21 138
138








