З а д а ч а 16. Сопротивление линии передачи 300 Ом. Какое напряжение должно быть на клеммах генератора, чтобы потери в линии не превышали 4 % от потребляемой мощности, равной 25 кВт?
Дано:
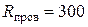 Ом; Ом;
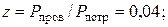 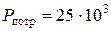 Вт.
Найти: Вт.
Найти: 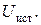
| Решение.
Схема электрической цепи показана на рис. 15. Согласно формуле (19) с учетом условия задачи сила тока в цепи
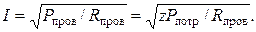 (38) (38)
|
Мощность, передаваемая от источника, расходуется на потребление и потери в проводах (выражение (37)): 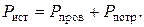 Отсюда, учитывая условие задачи, получим:
Отсюда, учитывая условие задачи, получим: 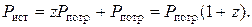
Согласно формуле (17) 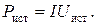 Приравнивая эти соотношения друг к другу, получим:
Приравнивая эти соотношения друг к другу, получим: 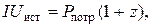 откуда
откуда
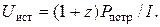 (39)
(39)
Подставив равенство (38) в выражение (39), получим: 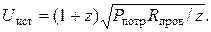 Подставив в это выражение данные задачи, найдем:
Подставив в это выражение данные задачи, найдем: 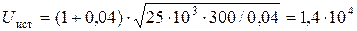 В.
В.
Ответ: 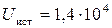 В.
В.
З а д а ч а 17. Напряжение на шинах электростанции 10 кВ, расстояние от станции до потребителя 400 км. Станция должна передать потребителю мощность 100 кВт. Потери напряжения в подводящих проводах не должны превышать 4 %. Вычислить массу подводящих проводов, если они изготовлены из меди и имеют цилиндрическую форму.
Дано:
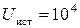 В; В;
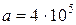 м; м;
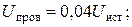 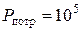 Вт; Вт;
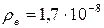 Ом·м; Ом·м;
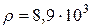 кг/м3.
Найти: кг/м3.
Найти: 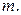
| Решение.
Схема электрической цепи показана на рис. 15.
Массу проводов рассчитаем по формуле 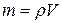 через плотность меди r и объем цилиндра: через плотность меди r и объем цилиндра: 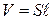 , где , где 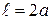 – длина проводов в двухпроводной линии (см. рис. 15); – длина проводов в двухпроводной линии (см. рис. 15); 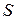 – площадь поперечного сечения проводов, которая выражается из формулы (2): – площадь поперечного сечения проводов, которая выражается из формулы (2): 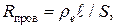 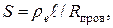 где где 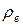 – удельное сопротивление меди. Объединив эти соотношения, получим: – удельное сопротивление меди. Объединив эти соотношения, получим:
|
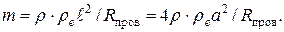 (40)
(40)
Чтобы найти сопротивление проводов, используем условие задачи 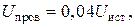 уравнение (36):
уравнение (36):
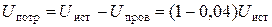 (41)
(41)
и закон Ома для однородного участка цепи (7):
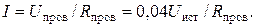 (42)
(42)
Согласно формулам (17), (41) и (42) получаемая потребителем мощность 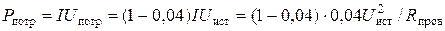 . Отсюда
. Отсюда
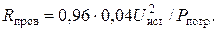 (43)
(43)
Подставив соотношение (43) в формулу (40), найдем: 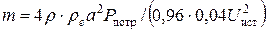 . Произведя численный расчет, получим:
. Произведя численный расчет, получим: 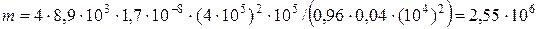 кг.
кг.
Ответ: 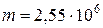 кг.
кг.
4. ПРАВИЛА КИРХГОФА
 2020-05-21
2020-05-21 144
144








