Для аппроксимации (замены) первой производной можно воспользоваться формулами:
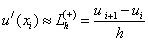 - правая разностная производная,
- правая разностная производная,
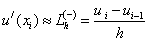 - левая разностная производная,
- левая разностная производная,
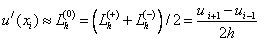 - центральная разностная производная.
- центральная разностная производная.
т.е., возможно множество способов аппроксимации производной.
Все эти определения следуют из понятия производной как предела: 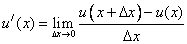 .
.
Опираясь на разностную аппроксимацию первой производной можно построить разностную аппроксимацию второй производной:
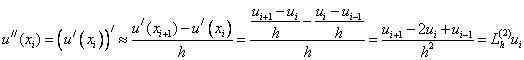 (3)
(3)
Аналогично можно получить аппроксимации производных более высокого порядка.
Определение. Погрешностью аппроксимации n- ой производной называется разность: 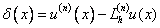 .
.
Для определения порядка аппроксимации используется разложение в ряд Тейлора.
Рассмотрим правую разностную аппроксимацию первой производной:
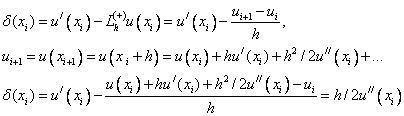
Т.е. правая разностная производная имеет первый по h порядок аппроксимации.
Аналогично и для левой разностной производной.
Центральная разностная производная имеет второй порядок аппроксимации.
Аппроксимация второй производной по формуле (3) также имеет второй порядок аппроксимации.
Для того чтобы аппроксимировать дифференциальное уравнение необходимо в нем заменить все производные их аппроксимациями. Рассмотрим задачу (1), (2) и заменим в(1) производные:
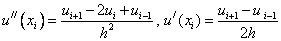 .
.
В результате получим:
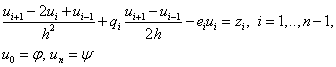 (4)
(4)
Порядок аппроксимации исходной задачи равен 2, т.к. вторая и первая производные заменены с порядком 2, а остальные – точно.
Итак, вместо дифференциальных уравнений (1), (2) получена система линейных уравнений для определения 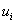 в узлах сетки.
в узлах сетки.
Схему можно представить в виде:

т.е., получили систему линейных уравнений с матрицей:

Данная матрица является трехдиагональной, т.е. все элементы, которые расположены не на главной диагонали и двух прилегающих к ней диагоналях равны нулю.
Решая полученную систему уравнений, мы получим решение исходной задачи.
Для решения таких СЛАУ имеется экономичный метод прогонки.
Рассмотрим метод прогонки для СЛАУ:
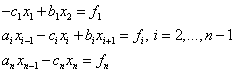 (1)
(1)
Решение данной системы ищем в виде:
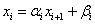 (2)
(2)
Подставляя в первое уравнение, получим:

Здесь учтено, что данное соотношение должно выполняться при любом 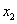
Так как
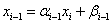 , (3)
, (3)
то подставляя (3) во второе уравнение, получим:
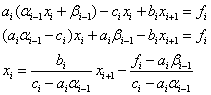
Сравнивая с (2) получим
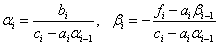 .
.
Таким образом, можно найти все 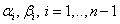 .
.
Тогда из последнего уравнения (1) находим:
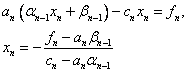
Затем последовательно находим:
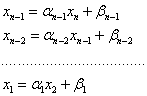
Таким образом, алгоритм метода прогонки можно представить в виде:
1) Находим 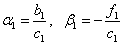
2) Для i=1,n-1: 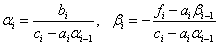 (4)
(4)
3) Находим 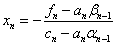
4) Для i=n-1 до 1 находим: 
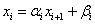
Шаги 1),2) – прямой ход метода прогонки, 3),4) – обратный ход метода прогонки.
Теорема. Пусть коэффициенты ai, bi системы уравнений при i =2, 3, …, n–1 отличны от нуля и пусть
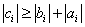 при i =1, 2, 3, …, n. Тогда прогонка корректна и устойчива.
при i =1, 2, 3, …, n. Тогда прогонка корректна и устойчива.
При выполнении этих условий знаменатели в алгоритме метода прогонки не обращаются в нуль и, кроме того, погрешность вычислений, внесенная на каком либо шаге вычислений, не будет возрастать при переходе к следующим шагам. Данное условие есть ни что иное, как условие диагонального преобладания.
Для нашей краевой задачи имеем:

Тогда: 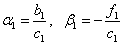 ,
, 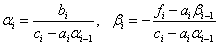 ,
,
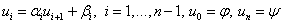
Для нашей задачи условие устойчивости имеет вид:
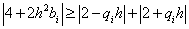 .
.
Пусть
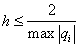 . (6)
. (6)
Тогда 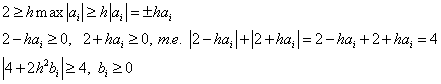
Пример. Найти решение задачи:
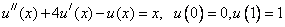
Выпишем разностную схему
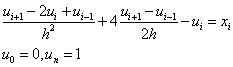
Условие устойчивости примет вид 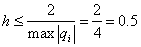
Возьмем 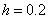 .
.
Тогда 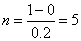
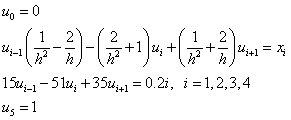
Или
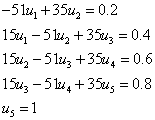
Формулы прогонки были получены для СЛАУ (1):
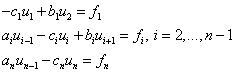
Здесь x замены на u.
Следовательно,
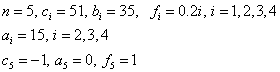
Решим СЛАУ методом прогонки. Вычисления оформим в виде таблицы:
| I | ai | ci | bi | fi | alfai | betai | u i |
| 1 |
| 51 | 35 | 0.2 | 0.6863 | -0.0039 | 0.4701 |
| 2 | 15 | 51 | 35 | 0.4 | 0.8598 | -0.0113 | 0.6906 |
| 3 | 15 | 51 | 35 | 0.6 | 0.9186 | -0.0202 | 0.8164 |
| 4 | 15 | 51 | 35 | 0.8 | 0.9403 | -0.0296 | 0.9107 |
| 5 | 0 | -1 |
| 1 |
|
| 1.0000 |
Порядок вычислений по формулам (4):
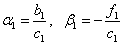
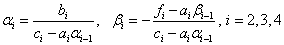
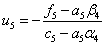
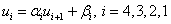
Ответ в столбце ui.
Если забыли формулы, то их можно легко вывести. Главное запомнить основную формулу:
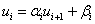
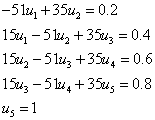
Прямой ход

Обратный ход
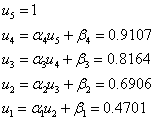
На практике часто граничные условия могут иметь более общий вид.
Рассмотрим следующую краевую задачу:
Найти решение ОДУ 2-го порядка
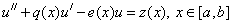 ,
,
удовлетворяющую краевым условиям:

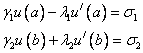
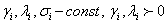
В этом случае при построении разностной схемы необходимо еще аппроксимировать и краевые условия.
Аппроксимация:
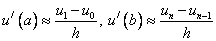
В результате получим разностную схему:
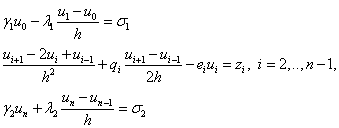
Или
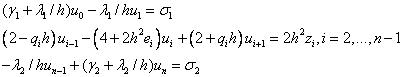
Мы получили СЛАУ типа (5) с трехдиагональной матрицей, решение которой также можно найти методом прогонки.
Лекция 8-9. Числовые ряды. Сходимость и расходимость числовых рядов. Признак сходимости Даламбера. Знакопеременные ряды. Абсолютная и условная сходимость рядов. Интегральный признак Коши. Признак Лейбница. Степенные ряды. Ряды Фурье.
Основные понятия.
Числовым рядом называется выражение вида а1+а2+а3+…+аn+…, где а1, а2, а3,…аn, , называемые членами ряда, образуют бесконечную последовательность.
Ряд называется сходящимся, если последовательность его частичных сумм
S1 = a1,
S2 = a1 + a2
S3 = a1 + a2 + an
…………………
S1 = а1+а2+а3+…+аn
при n ®µ имеет конечный предел: 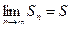 . Этот предел называется суммой сходящегося ряда. Если конечный предел
. Этот предел называется суммой сходящегося ряда. Если конечный предел 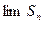 не существует, то ряд называется расходящимся.
не существует, то ряд называется расходящимся.
· Необходимый признак сходимости ряда. Достаточные признаки сходимости рядов с положительными членами.
Ряд может сходиться только при условии, что его общий член an при неограниченном увеличении номера n стремиться к нулю: 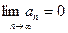 - это необходимый признак сходимости ряда.
- это необходимый признак сходимости ряда.
Если же 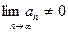 , то ряд расходиться – это достаточный признак расходимости ряда.
, то ряд расходиться – это достаточный признак расходимости ряда.
Для знакоположительных числовых рядовимеют местоследующие достаточные признаки, по которым можно установить их сходимость или расходимость.
1. Признак сравнения. Если члены знакоположительного ряда
а1+а2+а3+…+аn+…, (1)
начиная с некоторого номера, не превосходят соответствующих членов ряда
b1+b2+b3+…+bn+…, (2)
то из сходимости ряда (2) следует сходимость ряда (1), а из расходимости ряда (1) следует расходимость ряда (2).
При исследовании рядов на сходимость и расходимость по этому признаку часто используются геометрическая прогрессия
a + aq + aq2 + aq3 + … + aqn +… (a > 0),
которая сходиться при ½q½ < 1 и расходиться при ½q½ ≥ 1, и гармонический ряд
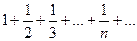 ,
,
Являющийся расходящимся рядом.
2. Признак Даламбера. Если для ряда (1) 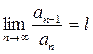 , то при l < 1 ряд сходиться, при l > 1 – расходиться (при l = 1 вопрос о сходимости остается нерешенным).
, то при l < 1 ряд сходиться, при l > 1 – расходиться (при l = 1 вопрос о сходимости остается нерешенным).
· Признак сходимости Лейбница.
Знакочередующимся рядом называется ряд вида
а1 - а2 + а3 - …+ (-1)n-1an + …, (1)
где а1, а2, а3,…аn - положительные числа.
Для знакочередующихся рядов имеет место следующий признак сходимости.
Признак Лейбница. Ряд (1) сходиться, если его слены монотонно убывают по абсолютной величине и общий член стремиться к нулю при n® µ/
· Абсолютная и условная сходимость знакопеременного ряда.
Ряд а1 +а2+а3+…+аn+… (1)
называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные числа.
Признак сходимости знакопеременного ряда. Если ряд
½а1 ½+½а2½+½а3½+…+½аn½+…, (2)
составленный из абсолютных величин членов ряда (1), сходится, то ряд (1) также сходиться.
Знакопеременный ряд (1) называется абсолютно сходящимся, если, сходиться ряд (2), составленный из абсолютных величин членов данного ряда (1).
Сходящийся знакопеременный ряд называется условно сходящимся, если ряд, составленный из абсолютных величин его сленов, расходиться..
· Степенные ряды.
Степенным рядом называется ряд вида
а0 + а1х + а2х2 + … + anxn + …, (1)
где а0, а1, а2, а3,…аn,… - постоянные числа, называемые коэффициентами ряда.
Областью сходимости степенного ряда называется совокупность всех значений х, при которых данный ряд сходится.
Нахождение области сходимости состоит из двух этапов.
1. Определяется интервал сходимости степенного ряда, т.е. интервал (-R,R) числовой оси, симметричный относительно точки х = 0 и обладающий тем свойством, что при всех ½х ½ < R – ряд сходиться и притом абсолютно, а при всех ½х ½ > R – ряд расходится. Для этого применяется признак Даламбера к ряду ½а0½ + ½а1½½х ½+ ½а2½½х2½ + … +½ an½½xn½ + …, члены которого есть абсолютные величины членов данного ряда (1).
2. Исследуется сходимость ряда (1) на концах интервала сходимости в точках х = -R и х = R.
Пример 1. Исследовать сходимость ряда
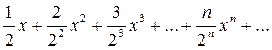
в точках х = 1, х = 3, х = - 2.
Решение.
При х = 1 данный ряд превращается в числовой 
По признаку Даламбера этот ряд сходиться, так как
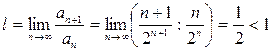
При х = 3 имеем ряд 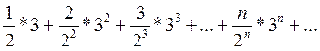
Применяя признак Даламбера, получим
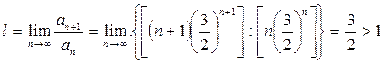 .
.
Следовательно, в точке х = 3 данный ряд расходится.
При х = -2 получаем следующий числовой ряд: -1 + 2 – 3 + 4 -..+ (-1)n n + …, который расходится (так как не выполняется необходимый признак сходимости ряда).
Пример 2. Исследовать на сходимость степенной ряд 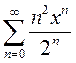 .
.
Решение. Здесь 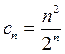 ,
, 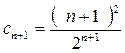 ; тогда радиус сходимости
; тогда радиус сходимости
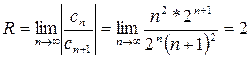 . Область сходимости -2 < x < 2. Исследуем сходимость ряда в граничных точках. При х = ± 2 степенной ряд принимает вид
. Область сходимости -2 < x < 2. Исследуем сходимость ряда в граничных точках. При х = ± 2 степенной ряд принимает вид
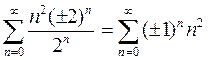 . Оба эти ряда расходятся, так как для них не удовлетворяется необходимый признак сходимости.
. Оба эти ряда расходятся, так как для них не удовлетворяется необходимый признак сходимости.
Ряды Тейлора и Маклорена
Если функция разложима в некоторой окрестности точки 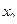 в степенной ряд по степеням
в степенной ряд по степеням 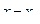 ,то этот ряд имеет вид:
,то этот ряд имеет вид:
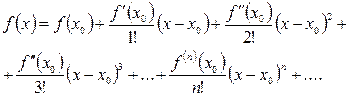 (1.1)
(1.1)
Ряд (1.1) называется рядом Тейлора для функции 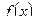 .
.
При 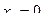 ряд (1.1) принимает вид:
ряд (1.1) принимает вид:
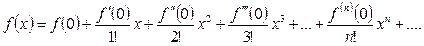 (1.2)
(1.2)
Ряд (1.2) называется рядом Маклорена для функции 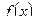 .
.
Таким образом, если функция разлагается в ряд по степеням 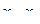 , то этот ряд является рядом Тейлора (или рядом Маклорена при
, то этот ряд является рядом Тейлора (или рядом Маклорена при 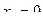 ). Очевидно, если функция разлагается в ряд Тейлора в точке
). Очевидно, если функция разлагается в ряд Тейлора в точке 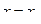 , то она имеет производные любого порядка в точке
, то она имеет производные любого порядка в точке 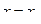 , т.е. бесконечно дифференцируема в точке
, т.е. бесконечно дифференцируема в точке 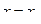
Пример 1. Записать два первых отличных от нуля члена ряда Тейлора функции 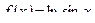 по степеням
по степеням 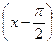 .
.
Решение. Найдём производные функции 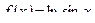 :
:
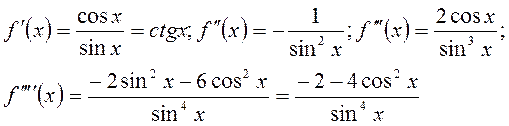
При 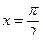 получим
получим
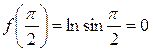 ;
; 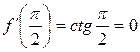 ;
; 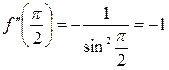 ;
;
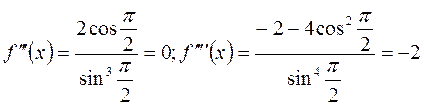 .
.
Запишем формально ряд Тейлора для функции 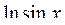 :
:
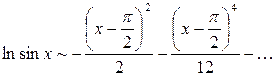 , или, после сокращения
, или, после сокращения 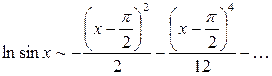 .
.
Разложение функций в ряд Маклорена
Имеют место следующие равенства:
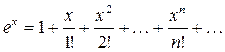 ,
, 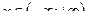 , (2.1)
, (2.1)
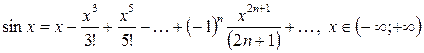 (2.2)
(2.2)
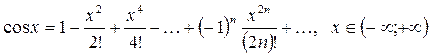 (2.3)
(2.3)
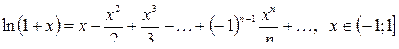 (2.4)
(2.4)
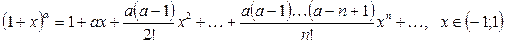 (2.5)
(2.5)
В частном случае, при  получаем функцию
получаем функцию 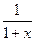 , которая является суммой геометрической прогрессии с первым членом
, которая является суммой геометрической прогрессии с первым членом  и со знаменателем
и со знаменателем
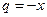 . Поэтому
. Поэтому
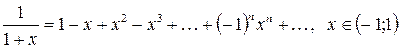 (2.6)
(2.6)
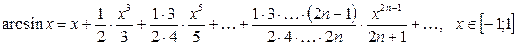 (2.7)
(2.7)
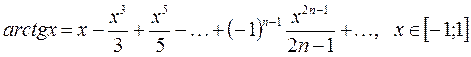 (2.8)
(2.8)
Пример 2. Разложить функцию 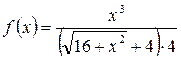 в ряд Маклорена и найти интервал сходимости ряда.
в ряд Маклорена и найти интервал сходимости ряда.
Решение. Преобразуем функцию 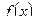 к виду:
к виду:
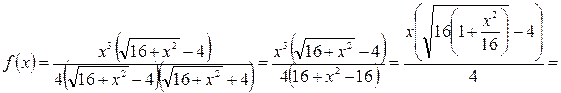
Разложим функцию 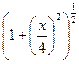 в степенной ряд по формуле (2.5)
в степенной ряд по формуле (2.5)
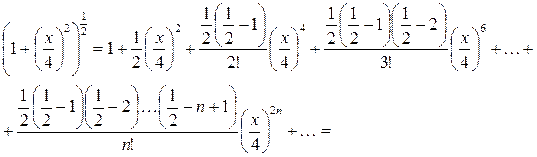
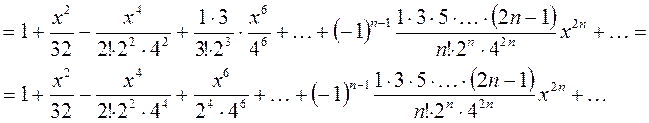
Это разложение верно при 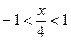 , т.е.
, т.е. 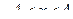 при. Тогда
при. Тогда
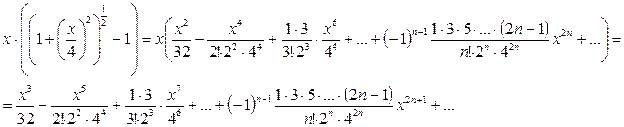
Этот ряд сходится при 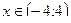 .
.
Пример 3. Разложить функцию 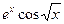 в ряд Маклорена и найти интервал сходимости ряда.
в ряд Маклорена и найти интервал сходимости ряда.
Решение: Внутри общего интервала сходимости 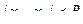
 имеет место формула
имеет место формула
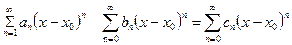 ,
,
где 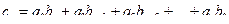 . Тогда, используя разложения (2.1) и (2.3), получим для
. Тогда, используя разложения (2.1) и (2.3), получим для 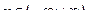
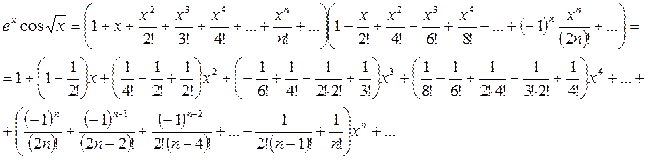
Итак:
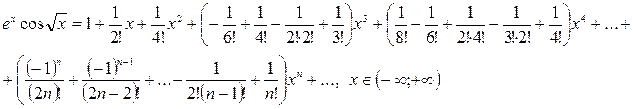
Вычисление определённых интегралов с помощью рядов
ПРИМЕР: Вычислить интеграл 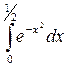 с точностью
с точностью 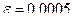 .
.
Решение: Разложим в ряд Маклорена подынтегральную функцию:
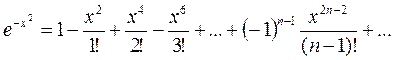 .
.
Это равенство имеет место при всех 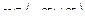 . Проинтегрировав его почленно в пределах от 0 до 1, получим:
. Проинтегрировав его почленно в пределах от 0 до 1, получим:
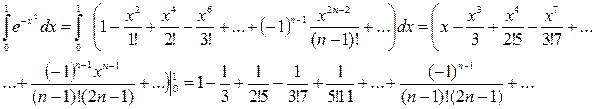 . (3.2)
. (3.2)
Так как вычисления нужно производить с тремя верными десятичными знаками, то погрешность не должна превышать 0,0005.
В правой части равенства стоит знакопеременный ряд. Если сумму знакопеременного ряда заменить суммой его первых n членов, то, как известно, возникающая при этом погрешность не превосходит модуля первого отброшенного члена. Поэтому в разложении (3.2) нужно оставить столько членов, чтобы первый отброшенный был меньше 0, 0005, причём следует учесть погрешности от округления бесконечных десятичных дробей, которые получатся в вычислениях.
Вычисляем члены нашего ряда, начиная со второго:
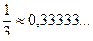 ;
;
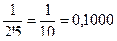 ;
;
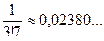 ;
;
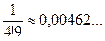 ;
;
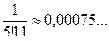 ;
;
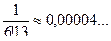 .
.
Следовательно, сохранив в сумме первые шесть членов, получим, что погрешность по абсолютной величине меньше первого отброшенного члена (седьмого члена) и она будет меньше, чем 0,00004, т.е. условие задачи выполнено.
Итак
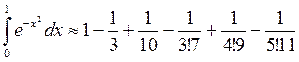 .
.
Теперь нужно вычислить приближённое значение 4 членов этой суммы (т.к. дробь 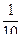 округлять не нужно). Со сколькими верными знаками следует вычислять каждую из 4-х бесконечных десятичных дробей
округлять не нужно). Со сколькими верными знаками следует вычислять каждую из 4-х бесконечных десятичных дробей 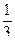 ;
; 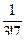 ;
; 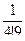 ;
; 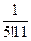 ?
?
Если каждую из них вычислять с тремя десятичными знаками, то погрешность вычислений для каждой дроби будет 0,0005, а для суммы 4-х дробей она будет равна 4 0,0005=0,002, т.е. превзойдёт заданную в условии погрешность.
Если вычисление дробей вести с четырьмя десятичными знаками, то погрешность вычислений для каждой дроби - 0,00005, а для их суммы 4 0,00005=0,0002.
Сложим погрешность вычислений 0,0002 с погрешностью 0,00004 от отбрасывания членов 0,0002+0,00004=0,00024<0,0005.
Итак, промежуточные вычисления выполняем с 4-мя верными знаками:
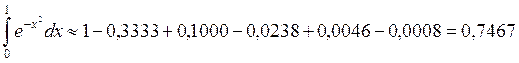
Округляя это число до трёх знаков, получим 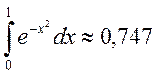 .
.
Лекция 10. Понятие события и вероятности события. Достовернее и невозможные события. Классическое определение вероятности. Теорема сложения вероятностей.
Комбинаторика
При решении ряда теоретических и практических задач требуется из конечного множества элементов по заданным правилам составлять различные комбинации и производить подсчет числа всех возможных таких комбинаций. Такие задачи принято называть комбинаторными, а раздел математики, занимающийся их решением, называется комбинаторикой. Комбинаторика широко применяется в теории вероятностей, теории массового обслуживания, теории управляющих систем и вычислительных машин и других разделах науки и техники. Основными элементами комбинаторики являются размещения, перестановки, сочетания.
Размещения.
Определение 1. Пусть дано множество, состоящее из n элементов. Размещением из n элементов по 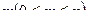 элементов называется упорядоченное множество, содержащее m различных элементов данного множества.
элементов называется упорядоченное множество, содержащее m различных элементов данного множества.
Из определения вытекает, что размещения из n элементов по m элементов – это все m – элементные подмножества, отличающиеся составом элементов или порядком их следования.
Число всех возможных размещений из n элементов по m элементов обозначают 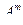 и вычисляют по формуле
и вычисляют по формуле 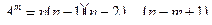 или
или 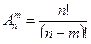 . (1)
. (1)
Здесь 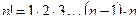 и
и 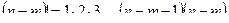 . Условимся считать 0! = 1, поэтому
. Условимся считать 0! = 1, поэтому 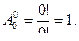
Пример 1. В группе из 30 учащихся нужно выбрать комсорга, профорга, физорга. Сколькими способами это можно сделать, если каждый из 30 учащихся комсомолец, член профсоюза и спортсмен?
Решение: искомое число способов равно числу размещений из 30 элементов по 3 элемента, т.е. 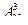 Положив по формуле (1)
Положив по формуле (1) 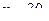
 получаем
получаем 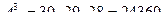
Перестановки
Определение 2. Перестановкой из n элементов по n элементов.
Так как каждая перестановка содержит все n элементов множества, то различные перестановки отличаются друг от друга только порядком следования элементов. Число всех возможных переустановок из n элементов обозначают 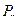 . Из определения перестановок следует
. Из определения перестановок следует
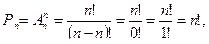 т.е.
т.е. 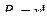 (2)
(2)
Пример 2. Сколькими способами можно расставлять на одной полке шесть различных книг?
Решении: Искомое число способов равно числу переустановок из 6 элементов, т.е.
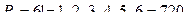
Сочетания
Определение 3. Пусть дано множество, состоящее из n элементов. Сочетанием из n элементов m элементов по 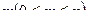 элементов называется любое подмножество, которое содержит m различных элементов данного множества.
элементов называется любое подмножество, которое содержит m различных элементов данного множества.
Следовательно, сочетания из n – элементного множества, причем различными подмножествами считаются только те, которые имеют неодинаковый состав элементов. Подмножества, отличающиеся друг от друга лишь порядком следования элементов, не считаются различными.
Число всех множественных сочетаний из n элементов по m элементов обозначают 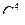 и вычисляются по формуле
и вычисляются по формуле 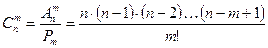 . (3)
. (3)
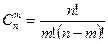 . (4)
. (4)
Пример 3. В бригаде из 25 человек нужно выделить четырех для работы на определенном участке. Сколькими способами это можно сделать?
Решение: т.к. порядок выбранных четырех человек не имеет значения, то это можно сделать 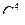
Способами. По формуле (4) находим 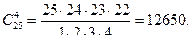
События, явления могут быть достоверными, невозможными и случайными. Те события, которые обязательно произойдут при осуществлении определённой совокупности условий (которую будем называть опытом или испытанием), называют достоверными (U). Событие, которое заведомо не произойдет, если будет осуществлена определенная совокупность условий, называют невозможным (V). События, которые при испытании могут произойти, а могут и не произойти, называют случайными (А, В, С...)
Различают события элементарные и составные. Множество всех элементарных событий, связанных с некоторым опытом, называется пространством элементарных событий (U). Каждое событие определяется как подмножество во множестве элементарных событий A. При этом те элементарные события из U, при которых событие А наступает (т.е. принадлежит подмножеству А), называются благоприятствующими событию А.
Пусть 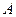 - случайное событие, связанное с некоторым опытом. Повторим опыт
- случайное событие, связанное с некоторым опытом. Повторим опыт 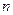 раз в одних и тех же условиях и пусть при этом событие
раз в одних и тех же условиях и пусть при этом событие 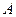 появилось
появилось 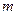 раз.
раз.
Определение 1. Отношение 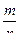 числа
числа 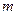 опытов, в которых событие
опытов, в которых событие 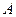 появилось, к общему числу
появилось, к общему числу 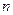 проведённых опытов называется частотой события
проведённых опытов называется частотой события 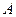 .
.
Оказывается, что при многократном повторении опыта частота события принимает значения, близкие к некоторому постоянному числу. Например, при многократном бросании игральной кости частота выпадения каждого из чисел очков от 1 до 6 колеблется около числа 1/6.
Свойство устойчивости частоты случайного события было подмечено и на явлениях демографического характера. Подсчитано, например, что частота рождения мальчика колеблется около числа 0,517.
Описанные в приведенных примерах явления, а также неоднократные наблюдения и других массовых явлений позволяют сделать вывод, что если опыт повторяется в одинаковых условиях достаточно большое количество раз, то частота некоторого события А приобретает статистическую устойчивость, колеблясь около некоторой постоянной величины р, к которой она все более приближается с увеличением числа повторений опыта.
Определение2. Постоянная величина р, к которой все более приближается частота событий А при достаточно большом повторении опыта, называется вероятностью события А и обозначается 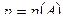
Классическое определение вероятности.
 2020-05-21
2020-05-21 1901
1901








