В тех точках, в которых дифференцируемы функции у = f (х) и у = g (х), такжеявляется дифференцируемой функция у = f (х) g (х), причем для всех таких точек выполняется равенство

Также принята упрощенная запись:
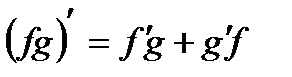
Следствие 1.
В тех точках, в которых дифференцируема функции у = f (х), такжеявляется дифференцируемой функция у = k f (х),где k – некоторое число, причем для всех таких точек выполняется равенство
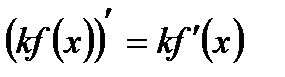
Коротко говорят: постоянный множитель можно выносить за знак производной.
Также принята упрощенная запись:

Следствие 2.
В тех точках, в которых дифференцируемы функции у = f (х) и у = g (х), такжеявляется дифференцируемой функция у = f (х) - g (х), причем для всех таких точек выполняется равенство

Производная частного
В тех точках, в которых функции у = f (х) и у = g (х) дифференцируемы и значение функции g не равно нулю, функция 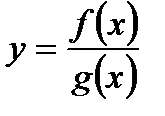 , такжеявляется дифференцируемой, причем для всех таких точек выполняется равенство
, такжеявляется дифференцируемой, причем для всех таких точек выполняется равенство
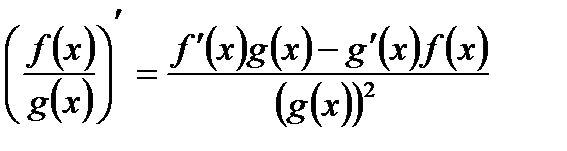
Упрощенная запись:
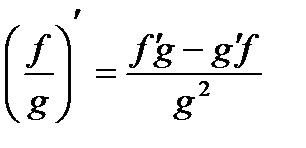
Пример 1. Найдите производную функции:
1) у = 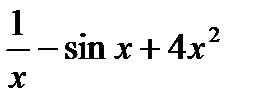
Решение. Пользуясь теоремой о производной суммы и следствием из теоремы о производной произведения, получаем:
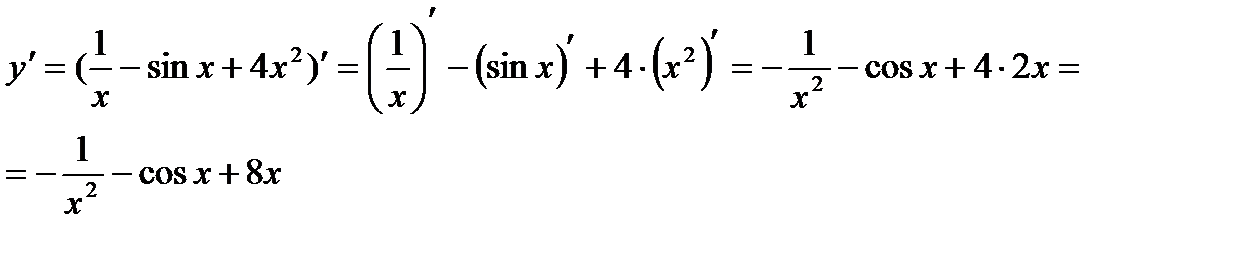
2) 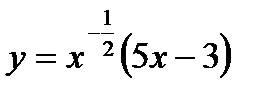
Решение.
По теореме о производной произведения получаем:

3) 
Решение.
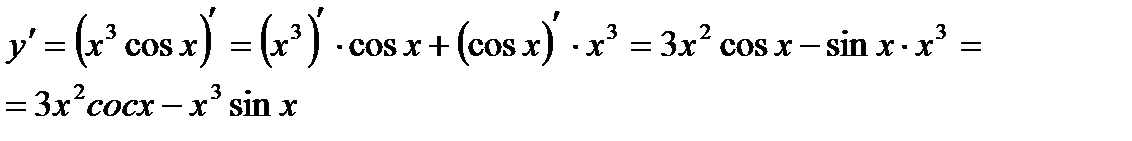
4) 
Решение.
По теореме о производной частного получаем:

Используя теорему о производной частного самостоятельно доказать, что
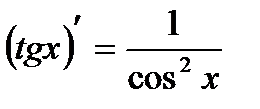
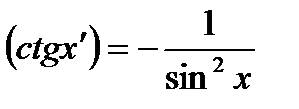
Производная сложной функции
Найти производную сложной функции можно с помощью следующей теоремы.
Если функция t=g(x) дифференцируема в точке 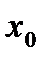 , а функция y=f(x) дифференцируема в точке
, а функция y=f(x) дифференцируема в точке 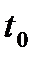 ,где
,где 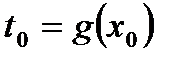 ,то сложная функция
,то сложная функция 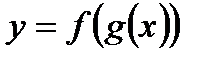 является дифференцируемой в точке
является дифференцируемой в точке  ,причем
,причем

Пример 2.
Найдите значение производной в точке 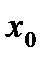 :
:
1) 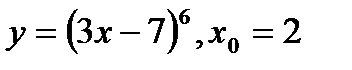
Решение
I - способ оформления данной задачи
Данная функция 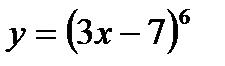 является сложной функцией
является сложной функцией 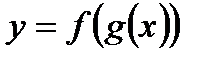 , где
, где 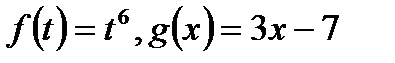
Поскольку 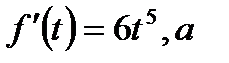
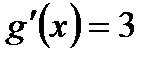 , то по теореме о производной сложной функции можно записать:
, то по теореме о производной сложной функции можно записать:

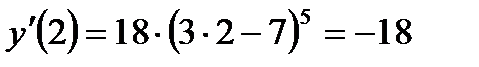
II - способ оформления данной задачи
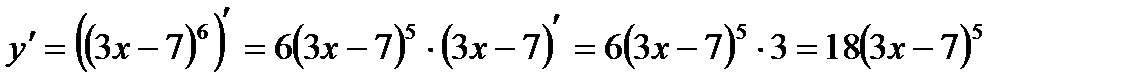
 2020-06-12
2020-06-12 124
124








