2020-06-12
216
Вопросы:
- Дайте определение производной функции.
- Что такое приращение аргумента, приращение функции?
- Как называют функцию, имеющую производную в некоторой точке?
- Как называется процесс вычисления производной?
- Чем является производная функции?
- Физический смысл производной и второй производной.
- Геометрический смысл производной.
- Дайте определение секущей и углового коэффициента.
- Опишите алгоритм нахождения производной.
Диктант
Вариант
Найдите производную функции:
1. У= 5;
2. У= 
3. 
Найдите угловой коэффициент касательной, проведенной к графику функции f в точке с абсциссой 
:
4. 
Касательная к графику функции f в точке с абсциссой имеет угловой коэффициент k. Найдите ,
если:
5. 
6. 
Вариант
Найдите производную функции:
1. У= 10;
2. У= 
3. 
Найдите угловой коэффициент касательной, проведенной к графику функции f в точке с абсциссой :
4. 
Касательная к графику функции f в точке с абсциссой имеет угловой коэффициент k. Найдите ,
если:
5. 
6. 
Учитель: Ребята, обменяйтесь тетрадями. Возьмите карандаши и проверяем правильность выполнения диктанта.
|
|
|
Ответы к диктанту:
1.Вариант
1. 
;
2. 
;
3. 
;
4. k = 5;
5. 
6. 
, 
2. Вариант
1. ;
2. 
;
3. 
;
4. k = 12;
5. 
;
6. 
Правила вычисления производных
Найдем, пользуясь определением, производную функции f(x)=x 
+x в точке x 
.
1) 
2) 
3) если 
, то значение выражения 
стремится к числу 
.Следовательно, при любом 
Так как 
- произвольная точка области определения функции
, то для любого 
выполняется равенство
, то есть 
Из ранее, изученного вам известно, что 
и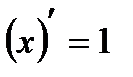 
. Таким образом, получаем:
.
Следовательно, производную функции 
можно найти как сумму производных функци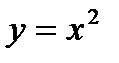й 
и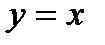 
.
Справедлива теорема:
«Производная суммы»
В тех точках, в которых дифференцируемы функции у = f (х) и у = g (х), такжеявляется дифференцируемой функция у= f(х)+g(х), причем для всех таких точек выполняется равенство
Коротко говорят: производная суммы равна сумме производных.
Также принята упрощенная запись:
Для упрощения нахождения производных приведем следующие теоремы.
