Закрепление изученного материала

 Решение задач из учебника

 

№36.1

1) У= ,

2) У= ,

№36.3

1) ,

3)   ,

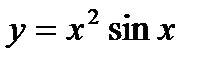№36.5

1)  , ;

2) , ;

№36.12

1) .

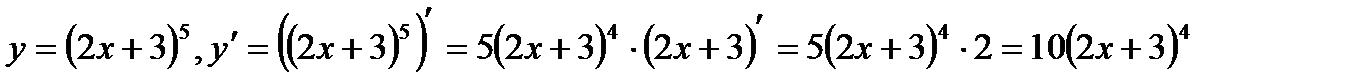№36.19

2) , ;

3) , .

УРОК по теме: «Производная суммы, разности,
произведения и частного функций»

 

Практическая работа.

Карточка №1. Найти производную функции в точке х₀

Карточка №2. Найти производную функции в точке х₀

Карточка №3. Найти производную функции в точке х₀

Вопросы:

1. Что называется приращением аргумента.

2. Что называется приращением функции.

3. В чем состоит геометрический смысл производной функции.

4. В чем состоит механический смысл производной функции.

5. Дайте определение производной функции f(x) в точке х₀.

Найдите производную следующих функций:

1.

2.

3.

Рассмотрим основные правила дифференцирования без доказательств.

Обозначим для краткости функции

Правило 1. Если функции U и V дифференцируемы в т. x, то их сумма (разность) дифференцируема в этой точке  (Слайд 2)

Пример:

Правило 2. Если функции U и V дифференцируемы в т. x, то их произведение дифференцируемо в этой точке  (Слайд 3)

Пример:

Следствие. Если функция дифференцируема в т. Х, а С –постоянная, то функция СU дифференцируема в этой точке и

(CU)'=CU'. (Слайд 4).

Пример:

Правило 3. Если функции U и V дифференцируемы в т.х и функция V не равна 0 в этой точке, то частное дифференцируемо в х и (Слайд 5)

Пример:

Вернемся к тем примерам которые рассматривали ранее. Теперь зная правила дифференцирования, как бы вы их решили?  

1.

2.

3.

Самостоятельная работа (дифференцированная)

Вариант 1 – на «3»

Вариант 2 – на «4»

Вариант 3 – на «5»

Вариант 1

1)

2)

3)

4)

Вариант 2 

1)

2)

3)

4)

Вариант 3

1)

2)

3)

4)

Урок: Таблица производных элементарных функций

Практическая работа

Найдите производную функции

1.	y=3x	8.	y=- +5	15.	y=sin2x	22.	y=cos3x
2.	y=4x2	9.	y=	16.	y=cos22x	23.	y=cos(4x-1)
3.	y=x-5	10.	y=	17.	y=	24.	y=ctg(x- )
4.	y=	11.	y=	18.	y=4x2+	25.	y=tg( -2x)
5.	y=	12.	y=4-x4	19.	y=	26.	y=
6.	y=x2+3sinx	13.	y=	20.	y=cos2x
7.	y=3x2+2x+5	14.	y=	21.	y=

 

После решения этих примеров на интерактивной доске высвечивается следующее задание для устного счета. Учащиеся выходят по одному к доске и стрелками устанавливают соответствие между левым и правым столбцами таблицы.