Плоское движение твердого тела слагается из поступательного движения, при котором все точки тела движутся так же, как полюс (А), и из вращательного движения вокруг этого полюса

Поступательное перемещение зависит от выбора полюса, а величина и направление угла поворота не зависят.

СКОРОСТЬ ТОЧКИ В

ПЛОСКОПАРАЛЛЕЛЬНОМ ДВИЖЕНИИ

При движении фигуры в плоскости положение её точек можно определить соотношением (рисунок):

.

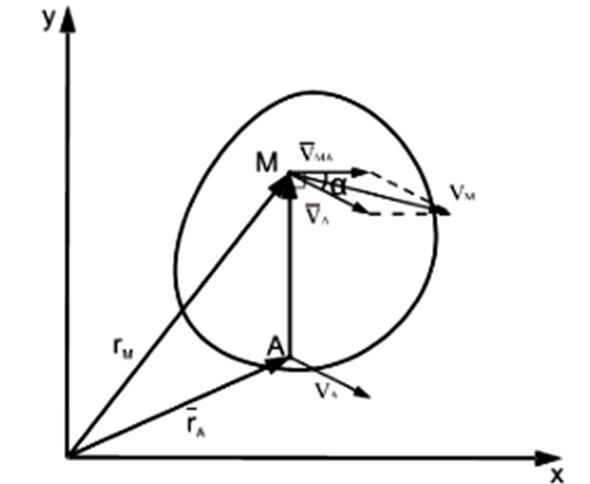
В данном случае точка A является полюсом.

ТЕОРЕМА О СКОРОСТЯХ ТОЧЕК ПЛОСКОЙ ФИГУРЫ

Скорость любой точки плоской фигуры при плоскопараллельном движении равна геометрической сумме скорости выбранного полюса и скорости точки во вращательном движении фигуры вокруг полюса.

Производная от вектора AM, постоянного по величине и переменного по направлению, численно равна скорости точки М при вращении ее вокруг точки А.

Вектор V_MA=ω⋅ AM перпендикулярен отрезку АМ.

Численную величину скорости точки М можно получить, если воспользоваться теоремой косинусов

или спроецировать векторное равенство (1) на выбранные оси координат

Из теоремы о скоростях точек плоской фигуры следует, что проекции скоростей точек плоской фигуры на ось, проходящую через эти точки, равны.

Это легко показывается в рассуждениях:

так как V_BA ⊥ AB, то и проекция V_BA на ось АХ равна нулю.

Следовательно, V_Bx = V_Ax