параллельных осей.
Рассмотрим случай, когда относительное движение тела является вращением с угловой скоростью w1 вокруг оси аа ¢, укрепленный на кривошипе ba вокруг bb ¢ оси с угловой скоростью w2.
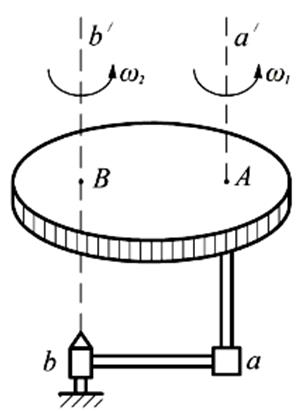
Если аа ¢ и bb ¢ параллельны, то движение тела будет плоско-параллельным по отношению к плоскости, перпендикулярной осям.
Исследуем отдельно случаи, когда вращения направлены в одну и в разные стороны
Вращения направлены в одну сторону.
Изобразим сечение (S) тела, плоскостью, перпендикулярной осям. Следы осей в сечении (S) изображены буквами А и В.

С – мгновенный центр скоростей и через нее проходит мгновенная ось вращения тела

 .
.
Если тело участвует одновременно в двух направленных в одну сторону вращениях вокруг параллельных осей, то его результирующее движение будет мгновенным вращением с абсолютной угловой скоростью w=w2+w1 вокруг мгновенной оси, параллельной данной.
Вращения направлены в разные стороны.

 ,
,

w = w2 - w1
С – мгновенный центр скоростей и мгновенная ось вращения, 
Векторы угловых скоростей при вращении вокруг параллельных осей складываются так же, как векторы параллельных сил.
Пара вращений
Рассмотрим частный случай, когда вращения вокруг параллельных осей направлены в разные стороны, но по модулю w1 = w2. Такая совокупность вращения называется парой вращений.


т.е. 
Тогда мгновенный центр скоростей будет, находится в бесконечности и все точки тела в данный момент, будут иметь одинаковые скорости 
Следовательно, результирующее движение тела будет поступательным (или мгновенно-поступательным) движением со скоростью V численно равной w1×АВ и направленной перпендикулярно плоскости, проходящей через векторы w1 и w2.
Примером такого движения является поступательное движение велосипедной педали относительно рамы велосипеда, являющееся результатом относительного вращения педали вокруг оси А, укрепленной на кривошипе ВА и переносного вращения кривошипа ВА вокруг оси В. Угловые скорости w1 и w2 в любой момент времени равны, так как j1 = j2.

Скорость поступательного движения педали

 2020-06-08
2020-06-08 157
157








