где х – расстояние между телами с зарядами q2 и q3,
получаем:
 | 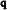 |  |  |  |  |  |  |  | |||||||||||
 | |||||||||||||||||||











 k = k
k = k
 |  |  |  | ||||||||
 |  | ||||||||||







 = => |q1| x2 = |q2| (r – x)2
= => |q1| x2 = |q2| (r – x)2



 q1 (r – x)2 r – x 2
q1 (r – x)2 r – x 2


 q2 x2 x
q2 x2 x





 q1 r – x r
q1 r – x r



 q2 x x
q2 x x








 q1 r r
q1 r r







 q2 x q1
q2 x q1



 q2
q2



 q2
q2


 q1 + q2
q1 + q2
 |








 3,33 10-9
3,33 10-9







 1,67 10-9 + 3,33 10-9
1,67 10-9 + 3,33 10-9
Ответ. х = 0,12 м.
№7 (565 Б)
На расстоянии r = 3 м друг от друга расположены два точечных отрицательных заряда q1 =  Кл и q2 =
Кл и q2 =  Кл. Когда в некоторой точке поместили заряд q0, то все три заряда оказались в равновесии. Найти заряд q0 и расстояние между зарядами q1 и q0 .
Кл. Когда в некоторой точке поместили заряд q0, то все три заряда оказались в равновесии. Найти заряд q0 и расстояние между зарядами q1 и q0 .
                      Дано:
q1 = -3 10-9 Кл
q2 = -12 10-9 Кл
F = 0
r = 3 м
e = 1 Дано:
q1 = -3 10-9 Кл
q2 = -12 10-9 Кл
F = 0
r = 3 м
e = 1
| Решение r1 F1,2 F1,0 F0,1 F0,2 - + - - q1 q0 - q2 г O X |
                                                         Найти q0 -?
r1 -? Найти q0 -?
r1 -?
|
Запишем условие равновесия для заряда q0: F0 = 0;





 F0 = F0,1 + F0,2
F0 = F0,1 + F0,2












 OX: F0 = F0,2 - F0,1; F0,2 = F0,1
OX: F0 = F0,2 - F0,1; F0,2 = F0,1










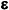


 F0,1 = k ; F0,2 = k
F0,1 = k ; F0,2 = k
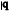 |  | ||||||||||||||||
 |  |  |  |  |  |  | |||||||||||































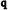

 k k ; e = 1
k k ; e = 1
















 3 10-9 12 10-9 1 4
3 10-9 12 10-9 1 4
 2020-06-08
2020-06-08 182
182








