Молекулярная физика и термодинамика

Задача 1. В сосуде находится m = 10 г углекислого газа при температуре t = 27 °С и давлении Р = 150 кПа.

1. Чему равна плотность газа при этих условиях?

2. Какова средняя квадратичная скорость молекул газа в этом случае?

3. Какая энергия приходится на вращательное движение всех молекул этого газа, а какая энергия – на поступательное движение?

Дано:

Решение:

1. При описании поведения идеального газа удобно использовать уравнение Менделеева – Клапейрона, которое связывает между собой термодинамические параметры состояния газовой системы. Оно имеет вид

По определению плотность  

Подставив в определение плотности отношение из уравнения Менделеева – Клапейрона, получим

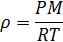
Все величины нам известны по условию задачи. Вычислим плотность газа при заданных условиях:

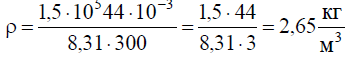
2. Вычислим среднюю квадратичную скорость молекул.

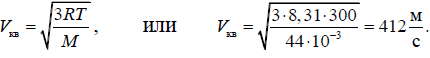
3. Внутренняя энергия идеального газа вычисляется по формуле

где i – число степеней свободы молекулы газа.

В нашем случае газ трехатомный, для него i = 6.

Из этих шести степеней свободы три степени приходятся на поступательное движение, а три степени – на вращательное движение:

i = i пост + i вр = 3 + 3.

Учитывая это, можем написать, что энергия вращательного движения всех молекул газа равняется

Определим эту энергию:

Электростатика

Задача 1. Две длинные, одноименно заряженные нити расположены на расстоянии r ₁ = 10 см друг от друга. Линейные плотности зарядов одинаковы и равны: τ₁ = τ₂ = 10 мкКл/м.

1. Найти модуль и направление напряженности результирующего поля в точке А, удаленной от каждой нити на расстояние а =10 см.

2. Какую работу А на единицу длины нити надо совершить, чтобы раздвинуть нити до расстояния r₂ = 20 см?

Дано: r =10 см r 2 = 20 см t1 =  t2 = τ = 10 мкКл/м a = 10 см

Найти: 1) E –? 2) A –?

 

Анализ:

Электростатические поля, создаваемые различными распределениями зарядов, по принципу суперпозиции складываются в каждой точке пространства.

Учитывая симметрию задачи, сделаем рисунок, расположив нити перпендикулярно плоскости чертежа.

Точка А удалена от обеих нитей на расстояние а = r ₁. Получили равносторонний треугольник. Для того чтобы найти направление вектора напряженности поля, создаваемого в точке А зарядом каждой нити, поместим в эту точку пробный заряд «+1» и определим, как поля нитей действуют на этот заряд.

Поскольку нити заряжены положительно, они будут отталкивать пробный заряд, и вектора 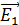и будут направлены так, как показано на рисунке.

Вектор напряженности суммарного поля, согласно принципу суперпозиции, находится по правилу параллелограмма.

Параллелограмм сил — геометрическое построение, выражающее закон сложения сил. Правило параллелограмма сил заключено в том, что вектор равнодействующей силы есть диагональ параллелограмма, построенного на векторах двух слагаемых сил, как на сторонах. Это выполняется оттого, что вектор равнодействующей силы есть сумма векторов складываемых сил, а сумма двух векторов есть диагональ параллелограмма, построенного на этих векторах.

Сила взаимодействия этих заряженных нитей зависит от расстояния между ними, поэтому работу сил электростатического поля при раздвижении нитей надо вычислять через интеграл.

Решение:

1. Из рисунка видно, что  направлен вправо, и модуль его можно найти как

И тогда получаем

2. Сила взаимодействия заряженных нитей зависит от расстояния между ними. Каждая нить создает поле, и это поле действует на заряд другой нити.

Напряженность поля первой нити

Работу этой силы можно вычислить как

Возьмем интеграл от этой функции. Все постоянные величины выносим за знак интеграла и получаем табличный интеграл, который равняется натуральному логарифму аргумента

Подставляем пределы интегрирования и окончательно получаем:

Используя данные задачи, получим:

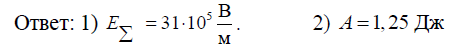
Задача 2. Пластины плоского воздушного конденсатора, расположенного горизонтально, заряжены одинаковым по модулю разноименным зарядом и отсоединены от источника напряжения.

Между пластинами находится в равновесии маленькая капелька, имеющая точечный заряд q ₀ = 10^–8 Кл и массу m = 0,010 кг.

1. Определите поверхностную плотность заряда пластин конденсатора σ.

2. Чему равна работа электростатических сил А при раздвижении пластин друг от друга с расстояния d ₁ = 3 см до d ₂ = 5 см? Площадь одной пластины S = 200 см².

Дано: q 0 = 10–8 Кл d 1 = 3 см d 2 = 5 см m = 10 мг = 10–5 г S = 200 см2

Найти: 1) σ–?  2) A –?

Решение:

Заряд находится в равновесии в поле конденсатора, следовательно, сила действия электрического поля равна силе тяжести капельки и противоположно направлена. Отсюда следует, что верхняя пластинка заряжена отрица тельно, а нижняя – положительно. Выполним рисунок.

Запишем условие равновесия капельки в векторном виде

В проекции на вертикальную ось OУ получим

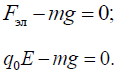
Отсюда можем выразить E:

Напряженность поля плоского конденсатора

но, учитывая предыдущую формулу, получим, что поверхностная плотность заряда пластины конденсатора

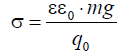
где ε = 1, так как конденсатор воздушный.

Вычислим искомую величину:

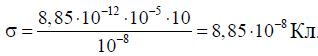
Поле конденсатора однородное, т. е. вектор  одинаков во всех точках пространства.

Будем считать, что одна пластина создает поле и оно действует на заряд другой пластины. Напряженность поля одной пластины находится следующим образом:

Но ε = 1, так как между пластинами конденсатора – воздух.

Сила, с которой электрическое поле первой пластины действует на заряд второй пластины, равна

где q₂ = σS – заряд другой пластины по модулю.

Поскольку поле однородное, тo F_эл = const, и работу можно вычислить следующим образом:

Угол между силой и перемещением равен 180⁰, так как пластины заряжены разноименными зарядами.