2020-06-29
87
17.4.1. Доказать формулы: 1) 
; 2)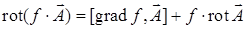 
.
Решение. 1)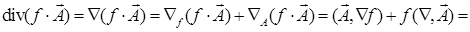 
.
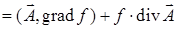2) 
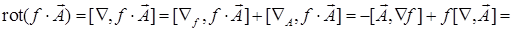
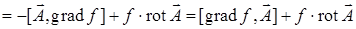. В этой выкладке мы учли, что векторное произведение меняет знак при перестановке сомножителей.
17.4.2. Вычислить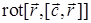 
, где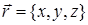 
– радиус вектор точки 
, а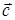 
– постоянный вектор.
Решение. По формуле для двойного векторного произведения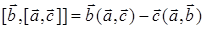 
запишем:
.
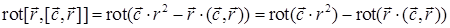Используя соотношение 2) примера 17.4.1, получим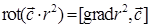 
, 
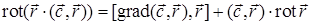. Теперь вычислим 
, 
, 
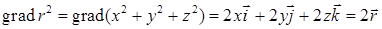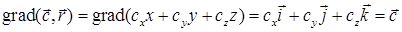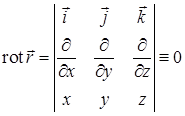. Отсюда 
.
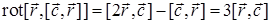17.4.3. Показать, что 
.
Решение. По формуле двойного векторного произведения (см. пример 17.4.2), получим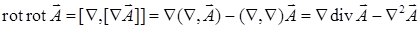 
. Первое слагаемое равно 
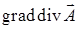, а во втором на вектор 
действует квадрат оператора Гамильтона. Это т. н. оператор Лапласа (или лапласиан), который обозначается символом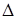 
и в декартовых координатах имеет вид 
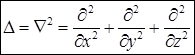. Оператор Лапласа применяется как к скалярным, так и к векторным полям. Таким образом, 
.
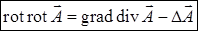17.4.4. Проверить, что векторное поле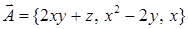 
является потенциальным, и найти его потенциал.
Решение.
|
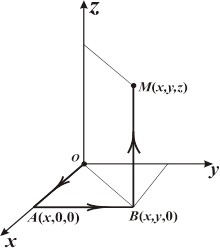
| Рис. 17.1 |
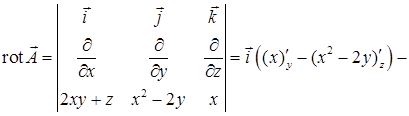
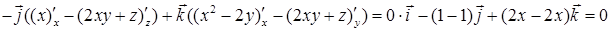. Значит, поле является потенциальным. Для вычисления потенциала воспользуемся формулой п. 17.2, приняв за точку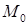 
начало координат и выбрав в качестве контура, соединяющего точку 
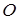с точкой 
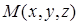, ломаную линию 
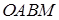со звеньями, параллельными координатным осям (рис. 17.1). Тогда 
, поскольку на отрезке 
, на отрезке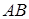 
координата 
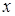не меняется 
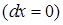, а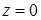 
, а на отрезке 
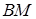не меняются значения координат 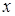и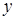 
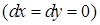. Далее, на отрезке 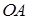функция 
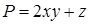равна нулю, т. к. 
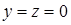. Учитывая все это, запишем 
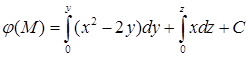. В обоих интегралах координата 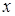полагается постоянной величиной, откуда 
.
|
|
|
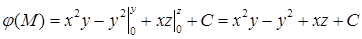17.4.5. Показать, что поле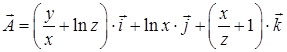 
является потенциальным, и вычислить работу поля вдоль контура, соединяющего точки 
и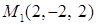 
.
Решение. Поле 
определено в области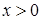 
, 
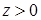. Ротор этого поля равен 
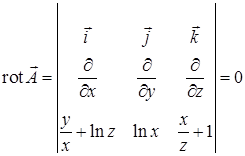, следовательно, поле является потенциальным. Найдем потенциал 
этого поля. Из равенства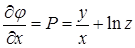 
следует, что 
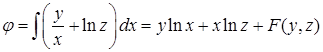, где 
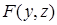– произвольная функция переменных 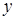и 
, выполняющая роль "константы" при интегрировании по переменной 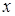. Для ее определения используем равенство 
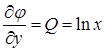, откуда, с учетом найденного выражения для 
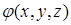, получим 
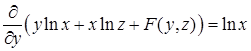, или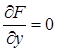 
, т. е. 
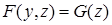. Функцию 
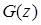определим из равенства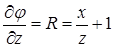 
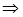
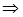
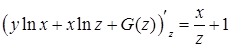, т. е. 
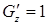, откуда 
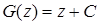. Итак, 
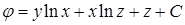, где 
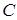– произвольная постоянная. Работа поля между точками 
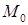и 
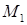равна
.
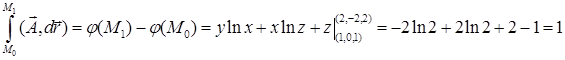17.4.6. Проверить, что поле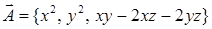 
является соленоидальным, и найти его векторный потенциал.
Решение.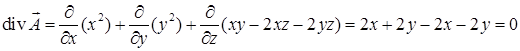 
, поэтому поле является соленоидальным. Следуя процедуре, описанной в п. 17.3, выберем 
, тогд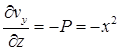а 
, 
, откуда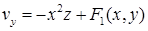 
, 
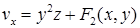, где 
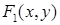и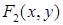 
– произвольные функции. Мы еще не использовали уравнение 
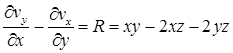, что, после подстановки найденных выражений для 
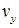и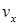 
, дает 
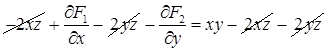. Положим теперь 
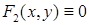, тогда 
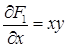, или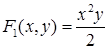 
. Итак, векторный потенциал данного поля равен 
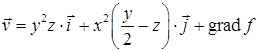, где 
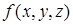– произвольная функция.
17.4.7. Показать, что поле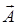 
, являющееся одновременно и потенциальным, и соленоидальным, удовлетворяет равенству 
.
|
|
|
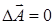Решение. Из формулы, полученной в примере 17.4.3, следует, что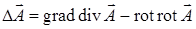 
. Если векторное поле является одновременно потенциальным и соленоидальным (такие поля называются гармоническими), то 
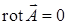и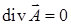 
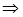
. Обратное утверждение неверно. Например, для 
, но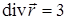 
.
Уравнение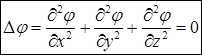 
называется уравнением Лапласа, а удовлетворяющие ему скалярные функции называются гармоническими. Очевидно, что потенциальное поле с гармоническим потенциалом само является гармоническим. Действительно, если 
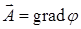, где 
, то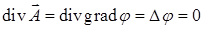 
, т. е. поле 
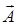является не только потенциальным, но и соленоидальным.
