2020-06-29
172
Векторное поле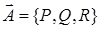 
называется соленоидальным, если оно является ротором некоторого векторного поля 
: 
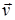. Поле 
называется векторным потенциалом поля 
.
Для того, чтобы, поле было соленоидальным в некоторой области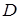 
, необходимо и достаточно, чтобы выполнялось одно из следующих условий:
1) 
в области ;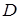
2) поток через любую кусочно-гладкую замкнутую поверхность 
равен нулю: 
;
3) поток поля через любую кусочно-гладкую поверхность не зависит от формы этой поверхности, а зависит только от контура 
, который является границей поверхности 
(рис. 16.1).
Векторный потенциал поля определяется с точностью до градиента произвольной дифференцируемой функции: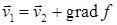 
, где 
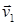и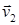 
– два векторных потенциала одного и того же поля .
Этим обстоятельством пользуются при отыскании векторного потенциала. Именно, полагают одну из компонент поля 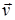равной нулю. Пусть, для определенности 
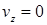, тогда из равенства 
или, в подробной записи, 
следует, что 
, 
, 
. Интегрируя эту систему, получаем некоторый потенциал 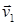данного поля . Общее решение имеет вид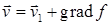 
, где 
– любая дифференцируемая функция.
В заключение отметим, что произвольное непрерывно дифференцируемое векторное поле можно представить в виде суммы потенциального и соленоидального полей.
