Векторное поле 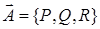 называется потенциальным, если оно является градиентом некоторого скалярного поля
называется потенциальным, если оно является градиентом некоторого скалярного поля 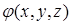 , т. н. потенциала векторного поля
, т. н. потенциала векторного поля  :
: 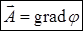 , или
, или 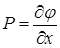 ,
, 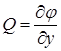 ,
, 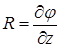 .
.
Для того, чтобы, поле  было потенциальным в некоторой области
было потенциальным в некоторой области 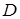 , необходимо и достаточно, чтобы выполнялось одно из следующих условий:
, необходимо и достаточно, чтобы выполнялось одно из следующих условий:
1) 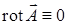 в области
в области 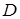 ;
;
2) циркуляция по любому кусочно-гладкому замкнутому контуру 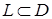 равна нулю:
равна нулю: 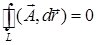 ;
;
3) работа векторного поля вдоль контура, соединяющего точки 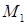 и
и  из области
из области 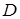 , не зависит от этого контура, а является функцией начальной и конечной точки:
, не зависит от этого контура, а является функцией начальной и конечной точки: 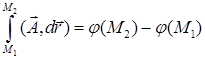 .
.
Последняя формула, аналогичная формуле Ньютона-Лейбница для определенного интеграла, позволяет найти потенциал векторного поля: 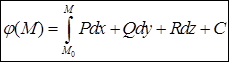 . Здесь
. Здесь 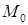 – начальная точка с фиксированными координатами
– начальная точка с фиксированными координатами 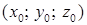 ;
; 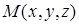 – текущая точка области
– текущая точка области 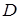 ;
; 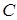 – произвольная постоянная. Для вычисления интеграла в качестве контура обычно выбирают ломаную линию со звеньями, параллельными координатным осям.
– произвольная постоянная. Для вычисления интеграла в качестве контура обычно выбирают ломаную линию со звеньями, параллельными координатным осям.
Заметим, что если поле 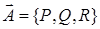 потенциально, выражение
потенциально, выражение 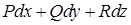 является полным дифференциалом функции
является полным дифференциалом функции 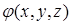 .
.
 2020-06-29
2020-06-29 171
171








