Задачи для самостоятельного решения

ДИСТАНЦИОННОЕ ОБУЧЕНИЕ

16.4.1.  Найти 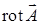, если: а) 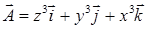; б) .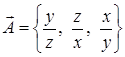

16.4.2. Решить задачу 14.5.5 б) с помощью формулы Стокса.

16.4.3. Найти циркуляцию векторного поля 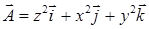 по сечению сферы  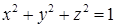плоскостью  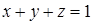в положительном направлении обхода относительно вектора .

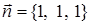16.4.4. Вычислить циркуляцию вектора 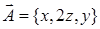 вдоль контура  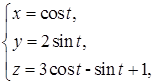пробегаемого в направлении возрастания параметра . Вычисления произвести непосредственно и по формуле Стокса.

16.4.5. Найти циркуляцию векторного поля 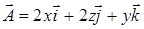 по ломаной 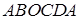, где 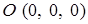, , 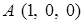, , 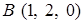 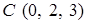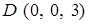— вершины прямоугольного параллелепипеда. При вычислении по теореме Стокса в качестве поверхности, опирающейся на контур, выберите часть поверхности этого параллелепипеда.

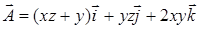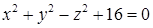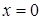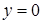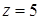16.4.6. Вычислить циркуляцию векторного поля  по контуру, вырезанному из двуполостного гиперболоида  плоскостями ,  и  при .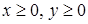

 

Ответы.

16.4.1. а) 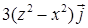; б) 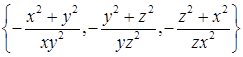. 16.4.3. 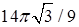. 16.4.4. 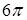.   16.4.5. 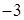.   16.4.6. .

ЧАСТЬ Б)

ДТСТАНЦИОННОЕ ОБУЧЕНИЕ

 СКАЛЯРНЫЕ И ВЕКТОРНЫЕ ПОЛЯ

Вычисление дифференциальных операций с помощью

Оператора Гамильтона

Градиентом скалярного поля 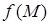 называется вектор , координаты которого в декартовой системе определяются как частные производные функции 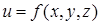 по соответствующим переменным: 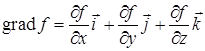. Свойства градиента перечислены в [1], 21.1.2.

Операцию нахождения градиента функции 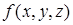 можно представить при помощи т. н. оператора Гамильтона  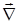(этот символ читается набла): 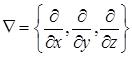. Оператор Гамильтона является векторным дифференциальным оператором первого порядка, и он действует на функции, расположенные справа от него. Так, градиент можно записать в виде . Дивергенцию можно рассматривать как скалярное произведение символа "набла" и векторного поля : 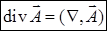. Ротор можно представить как векторное произведение: .

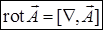При вычислениях с участием оператора Гамильтона важно помнить, что, как любой дифференциальный оператор первого порядка, он обладает свойством линейности: 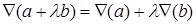. Здесь  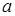и 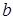 – выражения, зависящие от координат точки, а  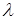– постоянная величина.

При действии символа "набла" на произведение двух величин (скалярных или векторных), зависящих от координат, применяется правило производной произведения: 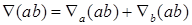. Запись символа "набла" в виде  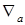показывает, что оператор Гамильтона действует на сомножитель  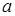и не действует на 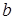. После этого каждое слагаемое необходимо переписать так, чтобы за оператором Гамильтона находилась только та величина, на которую он действует.