Эквивалентные виды записи ОДУ первого порядка

3 4 5 6 7 8 9

– ОДУ 1 порядка.

– разрешенное относительно

– другой вид записи ОДУ (в дифференциалах).

Определение. Решением ОДУ на интервале

называется всякая функция

, имеющая на этом интервале производную первого порядка и такая, что подстановка

и ее производной в дифференциальное уравнение обращает последнее в тождество по

на интервале

Например, функция является решением дифференциального уравнения на интервале .

Задача Коши. Задача отыскания решения дифференциального уравнения, удовлетворяющего заданному начальному условию .

Например, функция является решением дифференциального уравнения , удовлетворяющим начальному условию .

19.1.1. Теорема. Если непрерывна по совокупности аргументов, имеет непрерывную производную в окрестности т. , то решение задачи Коши существует и единственно в окрестности точки .

В уравнении функция определена и непрерывна во всех точках плоскости и имеет всюду . В силу теоремы 19.1.1 через каждую точку плоскости проходит единственная интегральная кривая этого уравнения.

19.1.2. Определение. Пусть выполняются условия теоремы 19.1.1.

Общим решением дифференциального уравнения в некоторой области существования и единственности решения задачи Коши называется однопараметрическое семейство функций , зависящих от переменной и одной постоянной 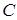(параметра), такое, что

1) при любом допустимом значении постоянной 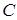функция является решением уравнения;

2) при любых начальных условиях , можно подобрать такое значение постоянной 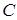, что решение будет удовлетворять начальному условию . При этом предполагается, что точка .

В процессе интегрирования дифференциального уравнения часто приходят к уравнению , неявно задающему общее решение уравнения. Уравнение называется общим интегралом дифференциального уравнения.

19.1.3. Определение. Частным решением дифференциального уравнения называется решение, получаемое из общего при каком-либо конкретном значении произвольной постоянной 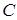(включая ).