Уравнения с разделяющимися переменными могут быть записаны в виде 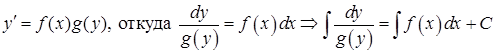 или
или
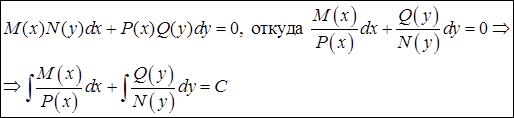
Замечание. Уравнения вида  приводятся к уравнениям с разделяющимися переменными заменой
приводятся к уравнениям с разделяющимися переменными заменой 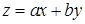 .
.
Решение некоторых типовых задач, рассматриваемых в аудитории
19.3.1. Решить уравнение  .
.
Решение.  .
.
Делим обе части уравнения на  , получим
, получим  , интегрируем
, интегрируем 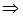
 - общее решение данного уравнения. При делении выражения на
- общее решение данного уравнения. При делении выражения на 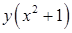 могло быть потеряно решение
могло быть потеряно решение 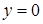 , но оно входит в общее решение при
, но оно входит в общее решение при 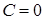 .
.
Ответ:  .
.
19.3.2. Решить уравнение 
Решение. Приведём уравнение к виду: 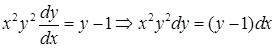 .
.
Делим обе части уравнения на выражение 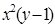 , получим
, получим 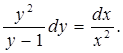
Переменные разделены. Интегрируем обе части уравнения: 
При делении выражения на  могли быть потеряны решения
могли быть потеряны решения 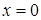 и
и 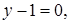 т. е.
т. е. 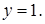 Очевидно,
Очевидно,  решение уравнения, а
решение уравнения, а 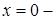 нет. Ответ:
нет. Ответ: 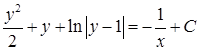 ;
;  .
.
19.3.3. Решить уравнение 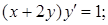

Решение. Обозначим  , тогда
, тогда 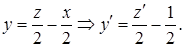
Подставляя 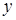 и
и 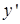 в данное уравнение, получим:
в данное уравнение, получим: 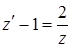 , откуда следует
, откуда следует
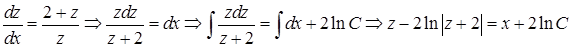 .
.
Возвращаясь к старым переменным, получим:
 — общий интеграл уравнения. Учитывая начальное условие, получим частный интеграл:
— общий интеграл уравнения. Учитывая начальное условие, получим частный интеграл: 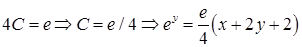 . Ответ:
. Ответ:  .
.
19.3.4. Решить уравнение 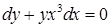 .
.
Решение. Разделим обе части уравнения на 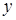 , получим
, получим  . При делении на
. При делении на 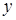 могло быть потеряно решение
могло быть потеряно решение 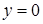 . Но это решение получается из общего решения при
. Но это решение получается из общего решения при 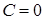 . Ответ:
. Ответ:  .
.
19.3.5. Решить уравнение 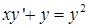 ;
; 
Решение. 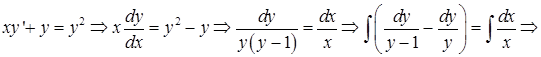
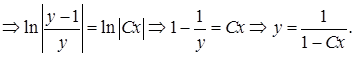
С учетом начального условия получим
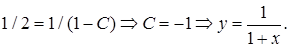 Ответ:
Ответ:  .
.
 2020-06-29
2020-06-29 117
117








