Пусть даны три вектора: 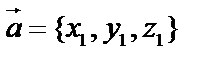 ,
, 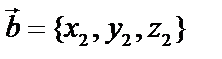 ,
, 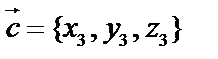 . Тогда смешанное (или векторно-скалярное) произведение –
. Тогда смешанное (или векторно-скалярное) произведение –  – скалярная величина, т.е. первые два вектора умножаются векторно, а результат – скалярно на третий вектор.
– скалярная величина, т.е. первые два вектора умножаются векторно, а результат – скалярно на третий вектор.
Геометрический смысл – 
 – объем параллелепипеда, построенного на векторах
– объем параллелепипеда, построенного на векторах  , которые образуют правую тройку. Если тройка левая, то
, которые образуют правую тройку. Если тройка левая, то  .
.
Свойства:
1.  – при циклической перестановке множителей смешанное произведение не меняется (не меняется параллелепипед).
– при циклической перестановке множителей смешанное произведение не меняется (не меняется параллелепипед).
2.  – знак меняется при перестановке двух сомножителей.
– знак меняется при перестановке двух сомножителей.
3.  , когда
, когда  компланарны. Действительно, параллелепипед выражается чисто в плоскость и
компланарны. Действительно, параллелепипед выражается чисто в плоскость и 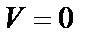 .
.
4. 


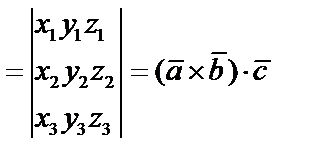
Это выражение смешанного произведения через координаты векторов.
5. Векторы 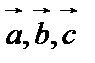 компланарны, если
компланарны, если 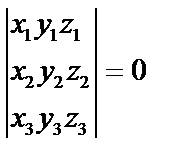 . Обычно смешанное произведение обозначают
. Обычно смешанное произведение обозначают 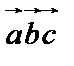 .
.
Глава 4. Аналитическая геометрия
Общее уравнение прямой на плоскости
Теорема. В декартовой системе координат каждая прямая на плоскости определяется уравнением первой степени.
Общее уравнение прямой на плоскости в декартовых координатах  . Если
. Если 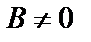 , то
, то  , обозначив
, обозначив  и
и  , получим уравнение прямой
, получим уравнение прямой  с угловым коэффициентом
с угловым коэффициентом 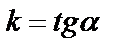 , где
, где  – угол прямой с осью О x; b – величина отрезка, отсеченного на оси O y. Если
– угол прямой с осью О x; b – величина отрезка, отсеченного на оси O y. Если  =0, то прямая параллельна оси O x и
=0, то прямая параллельна оси O x и  . Если
. Если  , то прямая перпендикулярна O x и
, то прямая перпендикулярна O x и 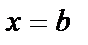 .
.
Пример.  ;
; 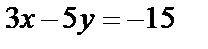 ;
; 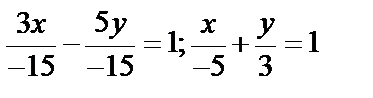 .
.
Преобразуем: 

 – угловой коэффициент.
– угловой коэффициент.

Уравнение прямой, проходящей через две точки. Угол между прямыми
Получим уравнение прямой, проходящей через  с угловым коэффициентом k.
с угловым коэффициентом k.
 .
.
 (1)
(1)
Получим уравнение прямой, проходящей через две точки  .
.
Из предыдущего уравнения: 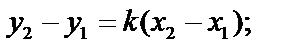
 . Подставим в (1):
. Подставим в (1):
 .
.
Если  (прямая параллельна оси ОХ), если
(прямая параллельна оси ОХ), если  (параллельна оси ОY).
(параллельна оси ОY).
Угол между прямыми с угловыми коэффициентами 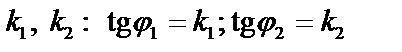 . Угол между прямыми:
. Угол между прямыми: 
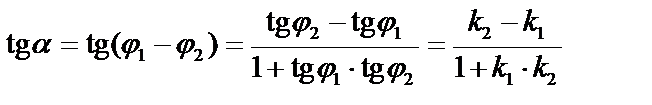 .
.
Условие параллельности прямых:  ; перпендикулярность:
; перпендикулярность:  .
.
 2020-06-29
2020-06-29 137
137








