Обратная матрица и ее вычисление

Теорема: всякая невырожденная матрица имеет обратную матрицу

Док-во: *см. ниже *

Пусть A - квадратная матрица n-ого порядка. Матрица  называется обратной матрицей к матрице A, если выполнено условие:

A · A−1 = A−1· A = E,

где Е - единичная матрица того же порядка, что и матрица А. Ма­трица  имеет те же размеры, что и матрица А.

Всякая матрица A, у которой detA ≠ 0, имеет обратную матрицу

n=2 

n=3 , где где A_ij - алгебраическое дополнение элемента a_ij:

Свойства обратной матрицы: 1)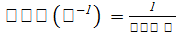

2)

3)

Док-во теоремы: пусть,причем detA ≠ 0

составим союзную матрицу и найдем произведение матриц А и А*

т.е. А А * = det А Е

Здесь мы использовали свойства 7 и 8 определителей. Аналогично убеждаемся, что А* · А = det А · Е.

Равенства перепишем в виде . Сравнивая результаты с определением обратной матрицы получаем , т.е.

Произведение матриц.

Т.е. элемент i-й строки и k-го столбца матрицы произведения С равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы k–го столбца матрицы В.

Если матрицы А и В квадратные одного размера, то произведения АВ и ВА всегда существуют. Легко показать, что А*Е=Е А=А, где А-квадратная матрица, Е- единичная матрица того же размера.

Матрицы А и В называются перестановычными, если АВ=ВА.

Если, конечно, написанные суммы и произведения матриц имеют смысл.

Для операции транспонирования верны свойства:

Умножение матрицы на число

Произведением матрицы А(m*n)=на число к называется матрица В(m*n)= такая, что. Записывают В=к*А