Определители, их свойства и методы вычислений

Каждой квадратной матрице A n-го порядка можно сопоставить число det A (ΙAΙ, Δ), называемое ее определителем (детерминантом).

Методы вычисления определителей:

Определитель 2-го порядка равен произведению элементов на главной диагонали минус произведение элементов на по побочной. Иллюстрируется схемой:

 

При вычислении определителя 3-го порядка удобно пользоваться правилом треугольников (или Саррюса):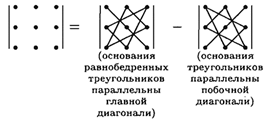

 

Свойства определителей:

1) «Равноправность строк и столбцов». Определитель не изменится, если его строки заменить столбцами, и наоборот:

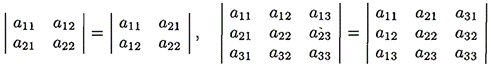Строки и столбцы называют также рядами определителя;

2) При перестановке двух параллельных рядов определитель меняет знак: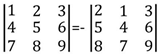

 

3) Определитель, имеющий два одинаковых ряда, равен нулю;

4) Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя:

5) Из свойств 3 и 4 следует, что определитель матрицы с двумя пропорциональными строками или столбцами равен нулю:

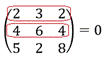
6) Если любой ряд состоит из нулей, то определитель равен нулю:

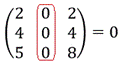
7) Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей:

и

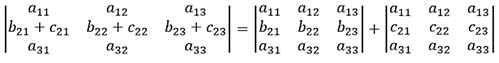
8) «Элементарные преобразования определителя». Определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на любое число:

9) Определитель матрицы треугольного вида равен произведению элементов, стоящих на главной диагонали:

 

Минором элемента a_ij называется определитель (n - 1)–го порядка, полученный вычеркиванием i-ой строки и j-го столбца

Пример:

Алгебраическим дополнением элемента a_ij называется число A_ij равное (-1)^i+jM_ij. То есть это тот же минор, только со знаком (+ или -).

A_{ij =} (-1)^i+jM_ij

10) «Разложение определителя по элементам некоторого ряда».

Это свойство является также способом вычисления определителей высоких порядков.

Определитель равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения:

 

11) Сумма произведений элементов какого-либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю: