Определенный интеграл. Пусть задана y=f(x) на отрезке [a;b]. Разобьем большой отрезок[a;b] на [xi-1;xi].

В каждом частном отрезке выберем произвольную точку Ci. В ней вычислим функцию Ci. Составим сумму (1)
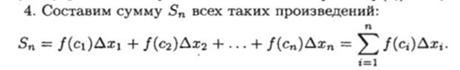
Сумма в виде(1) называется интегральной суммой y=f(x) на отрезке [a;b]. Обозначим через λ максимальное значение через Δxi: λ=max|Δxi|
Найдем lim интегральной суммы (1), когда n-> ∞ так, что λ->0. Если при этом интегральная сумма Sn имеет предел I, который не зависит ни от способа разбиения отрезка [a;b] на частичные отрезки, ни от выбора Сi в них, то число I называется определенным интегралом y=f(x) на отрезке [a;b] и обозначается

Геометрический смысл определенного интеграла. Пусть на отрезке [а;b] задана положительная f(x). Разобьем [а;b] на множество отрезков.
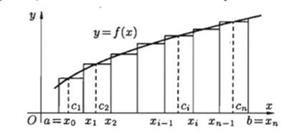
Найдем S фигуры, ограниченной сверху графиком функции f(x), а снизу осью Ох, сбоку прямыми x=a и x=b. Получаем площадь криволинейной трапеции.
f(Ci)Δxi=Si
Поэтому интегральная сумма (1) представляет собой площадь ступенчатой фигуры и приблизительно равна площади криволинейной трапеции. Если мы будем увеличивать число n, то интегральная сумма будет приближаться к площади криволинейной трапеции и в пределе даст эту искомую площадь. И поэтому 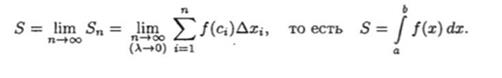
Итак, определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции.
Формула Ньютона-Лейбница. Теорема: Если y=f(x) непрерывна на [a;b], а F(x) – какая-либо ее первообразная, то имеет место формула

Определенный интеграл. Основные свойства.
Определенный интеграл. (см. Билет № 7)
 2020-06-29
2020-06-29 96
96








