1. Если с — постоянное число и функция ƒ(х) интегрируема на [a;b],то
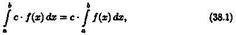
т. е. постоянный множитель с можно выносить за знак определенного интеграла.
Доказательство: Составим интегральную сумму для функции с • ƒ(х). Имеем:  Тогда отсюда вытекает,
Тогда отсюда вытекает, 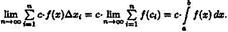 что функция с • ƒ(х) интегрируема на [а; b] и справедлива формула (38.1).
что функция с • ƒ(х) интегрируема на [а; b] и справедлива формула (38.1).
2. Если функции ƒ1(х)иƒ2(х) интегрируемы на [а;b], тогда интегрируема на [а; b] их сумма u
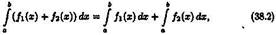 т. е. интеграл от суммы равен сумме интегралов.
т. е. интеграл от суммы равен сумме интегралов.
Доказательство: 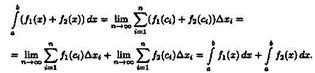
3.  Это свойство можно принять по определению. Это свойство также подтверждается формулой Ньютона-Лейбница.
Это свойство можно принять по определению. Это свойство также подтверждается формулой Ньютона-Лейбница. 
4. Если функция ƒ(х) интегрируема на [а; b] и а < с < b, то  т. е. интеграл по всему отрезку равен сумме интегралов по частям этого отрезка. Это свойство называют аддитивностью определенного интеграла (или свойством аддитивности).
т. е. интеграл по всему отрезку равен сумме интегралов по частям этого отрезка. Это свойство называют аддитивностью определенного интеграла (или свойством аддитивности).
Доказательство: При разбиении отрезка [а;b] на части включим точку с в число точек деления (это можно сделать ввиду независимости предела интегральной суммы от способа разбиения отрезка [а; b] на части). Если с = хm, то интегральную сумму можно разбить на две суммы:  Каждая из написанных сумм является интегральной соответственно для отрезков [а; b], [а; с]и[с; b]. Переходя к пределу в последнем равенстве при n → ∞ (λ → 0), получим равенство (38.3).
Каждая из написанных сумм является интегральной соответственно для отрезков [а; b], [а; с]и[с; b]. Переходя к пределу в последнем равенстве при n → ∞ (λ → 0), получим равенство (38.3).
Свойство 4 справедливо при любом расположении точек а, b, с (считаем, что функция ƒ (х) интегрируема на большем из получающихся отрезков).
Так, например, если а < b < с, то 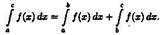 Отсюда
Отсюда 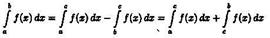 (использованы свойства 4 и 3).
(использованы свойства 4 и 3).
5. «Теорема о среднем». Если функция ƒ(х) непрерывна на отрезке [а; b], то существует точка с є [а; b] такая, что 

Доказательство:По формуле Ньютона-Лейбница имеем: 
где F'(x) = ƒ(х). Применяя к разности F(b)-F(a) теорему Лагранжа (теорему о конечном приращении функции), получим
F(b)-F(a) = F'(c)•(b-а) = ƒ(с)•(b-а).▲
Свойство 5 («теорема о среднем») при ƒ (х) ≥ 0 имеет простой геометрический смысл: значение определенного интеграла равно, при
некотором с є (а; b), площади прямоугольника с высотой ƒ (с) и основанием b- а (см. рис. 170). Число 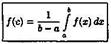 называется средним значением функции ƒ(х) на отрезке [а; b].
называется средним значением функции ƒ(х) на отрезке [а; b].
6. Если функция ƒ (х) сохраняет знак на отрезке [а; b], где а < b, то интеграл  имеет тот же знак, что и функция. Так, если ƒ(х)≥0 на отрезке [а; b], то
имеет тот же знак, что и функция. Так, если ƒ(х)≥0 на отрезке [а; b], то 
Доказательство:По «теореме о среднем» (свойство 5)  где с є [а; b]. А так как ƒ(х) ≥ 0 для всех х є [а; b], то и
где с є [а; b]. А так как ƒ(х) ≥ 0 для всех х є [а; b], то и
ƒ(с)≥0, b-а>0.
Поэтому ƒ(с)•(b-а) ≥ 0, т. е 
7. Неравенство между непрерывными функциями на отрезке [а; b], (a<b) можно интегрировать. Так, если ƒ1(x)≤ƒ2(х) при х є [а;b], то 
Доказательство:Так как ƒ2(х)-ƒ1(x)≥0, то при а < b, согласно свойству 6, имеем 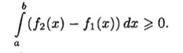
Или, согласно свойству 2, 
Отметим, что дифференцировать неравенства нельзя.
8. Оценка интеграла. Если m и М — соответственно наименьшее и наибольшее значения функции у = ƒ (х) на отрезке [а; b], (а < b),то 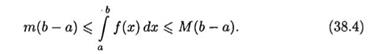
Доказательство: Так как для любого х є [а;b] имеем m≤ƒ(х)≤М, то, согласно свойству 7, имеем 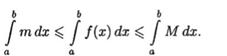
 Применяя к крайним интегралам свойство 5, получаем
Применяя к крайним интегралам свойство 5, получаем 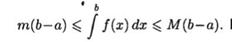 [1]
[1]
9. Модуль определенного интеграла не превосходит интеграла от модуля подынтегральной функции: 
Доказательство: Применяя свойство 7 к очевидным неравенствам -|ƒ(х)|≤ƒ(х)≤|ƒ(х)|, получаем  Отсюда следует, что
Отсюда следует, что 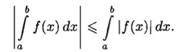
10. Производная определенного интеграла по переменному верхнему пределу равна подынтегральной функции, в которой переменная интегрирования заменена этим пределом, т. е. 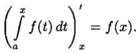
Доказательство: По формуле Ньютона-Лейбница имеем: 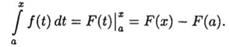 Следовательно,
Следовательно,  Это означает, что определенный интеграл с переменным верхним пределом есть одна из первообразных подынтегральной функции.
Это означает, что определенный интеграл с переменным верхним пределом есть одна из первообразных подынтегральной функции.
 2020-06-29
2020-06-29 85
85








