Решение простейших показательных уравнений
Показательное уравнение – это уравнение, в котором неизвестные (x) находятся в показателях каких-то степеней. И только там!
Примеры показательных уравнений:
· 5х+2 = 125
· 3х·2х = 8х+3
· 32х+4·3х-5 = 0
Обратите внимание, что в основаниях степеней находятся только числа, а в показателях – выражения с x.
Если, вдруг, в уравнении присутствует x где-нибудь, кроме показателя, например:
2х = 3+х,
это будет уже уравнение смешанного типа. Такие уравнения не имеют чётких правил решения. Их рассматривать не будем. Здесь мы будем разбираться с решением показательных уравнений в чистом виде.
Решение всех показательных уравнений сводится к решению уравнения  , где
, где 
Эти уравнения имеют единственный корень, так как справедлива следующая теорема:
Если  , то
, то 
Рассмотрим пример: 
Даже без теории, методом подбора данный пример решается элементарно.

Что же мы сделали? Фактически просто отбросили основания.
Действительно, если в показательном уравнении слева и справа стоят одинаковые числа в каких угодно степенях, эти числа можно убрать и приравнять показатели степеней.
!Важно: убирать основания можно только тогда, когда слева и справа числа-основания находятся без коэффициентов и слагаемых.
Например,
 или
или  – в данных примерах убирать основания нельзя.
– в данных примерах убирать основания нельзя.
Основные способы решения показательных уравнений
| Вид уравнения | Способ решения | Пример |
 |  |  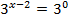   |
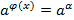 |  |      |
 |  |     |
  | · Логарифмирование обеих частей по любому основанию  По свойству логарифмов: По свойству логарифмов:   · По определению логарифма: · По определению логарифма:  | ·      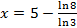 · ·    |
 | Деление обеих частей равенства на  или на или на   /: /:     |      |
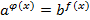 | Логарифмирование по любому основанию:   Раскрываем скобки и выражаем неизвестное Раскрываем скобки и выражаем неизвестное |  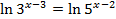     |
 | Замена  и решение квадратного уравнения с обратной подстановкой и решение квадратного уравнения с обратной подстановкой |    Пусть Пусть     Обратная замена Обратная замена     |
 | Вынесение числа с наименьшей степенью за скобки |     /:3 /:3     |
 | Решается аналогично предыдущему вынесением наименьшей степени |  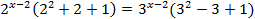  /:7 /:7  /: /:     |
Показательная функция, ее свойства и график
Показательной функцией называется функция вида  , где a – заданное число,
, где a – заданное число,  .
.
Показательная функция обладает следующими свойствами:
1) Область определения показательной функции – множество всех действительных чисел.
2) Множество значений показательной функции – множество всех положительных чисел.
3) Показательная функция  является возрастающей на множестве всех действительных чисел, если
является возрастающей на множестве всех действительных чисел, если  и убывающей, если
и убывающей, если 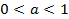 .
.
4) Нулей нет
5) Функция ни четная, ни нечетная (т.е. общего вида)
6) Наибольшего и наименьшего значения у функции нет.
7) Функция непериодична
8) Ограничена снизу, не ограничена сверху
 График функции:
График функции:
 (возрастающая)
(возрастающая) 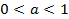 (убывающая)
(убывающая)

Пример 1:
Построить график функции 

| x | 0 | 1 | -1 |
| y | 1 | 2 |  |
Решение показательных уравнений:
Вопросы по теории:
1. Что такой показательная функция?
2. Почему накладываются ограничения a>0 и a  ?
?
Если  то
то  имеет смысл не для всех х
имеет смысл не для всех х
Например, 
Если 

3. Как выглядит график показательной функции?
4. Какие свойства показательной функции вы знаете?
Примеры на повторение:
1) 
2) 
3) 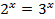
4) 
Решение:
1) 


2) 


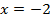
3) 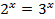

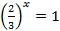


4) 

Пусть 



Произведем обратную замену:





Решить показательные уравнения:
1) 
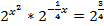



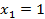
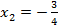
2) 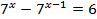





3) 




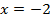
4) 

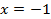
5) 

Вспомним, как раскрывается модуль:

Если  :
:

-x-4=-x+2
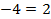
Корней нет
Если  :
:


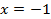
Если 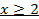
x-2=x+4
-2=4
Корней нет
Ответ: -1
 2020-06-29
2020-06-29 2329
2329