2020-06-29
58
Теорема. При движении плоской фигуры в каждый момент времени, если угловая скорость 
, существует единственная точка фигуры, скорость которой в данный момент равна нулю.
Доказательство. Пусть известны скорость некоторой точки А и угловая скорость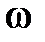 
плоской фигуры. Поворачивая вектор 
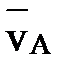на угол 
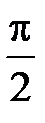по направлению 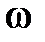построим полупрямую 
. На этой полупрямой отложим отрезок АР, равный
(4)
Таким образом построим точку Р. Покажем, что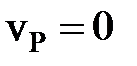 
. Принимая точку А за полюс, согласно формуле (2) запишем скорость точки Р:
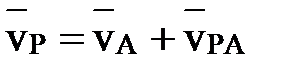
Вектор 
и направлен в сторону 
.
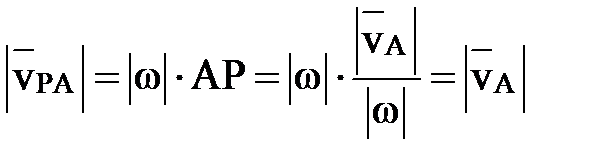
Итак, 
и .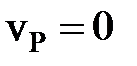
Теорема доказана.
Определение. Точка плоской фигуры, скорость которой в данный момент времени равна нулю, называется мгновенным центром скоростей. Мгновенный центр скоростей обычно обозначается буквой Р.
Мгновенный центр скоростей – это переменная точка: меняет своё положение как в пространстве, так и на плоской фигуре.
|
|
|
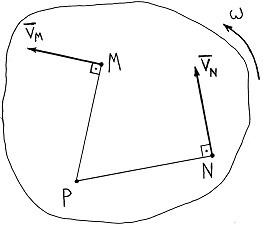Пусть в некоторый момент известны положение мгновенного центра скоростей и угловая скорость фигуры. Требуется найти скорость 
произвольной точки М фигуры. Примем мгновенный центр скоростей Р за полюс и согласно уравнению (2) запишем
Так как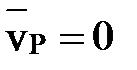 
, то
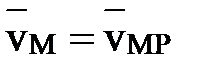
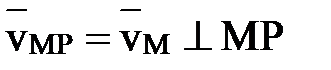в сторону .
(а)
Аналогично 
и 
(б)
Вывод:
В каждый момент времени скорости точек плоской фигуры можно определить как вращательные скорости при вращении вокруг мгновенного центра скоростей.
Из (а) и (б) следует, что
,
то есть скорости точек плоской фигуры пропорциональны расстояниям от точек до мгновенного центра скоростей.
Если в некоторый момент времени 
, то из уравнения (4) следует, что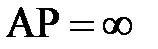 
. В этот момент мгновенного центра скоростей нет. Из уравнения (2) следует, что для любой точки М фигуры 
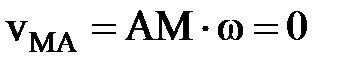и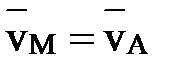 
, то есть скорость произвольной точки М фигуры равна скорости 
полюса.
Следовательно, если в некоторый момент времени , то скорости всех точек плоской фигуры в этот момент одинаковы и равны скорости полюса.
