Скорости точек плоской фигуры

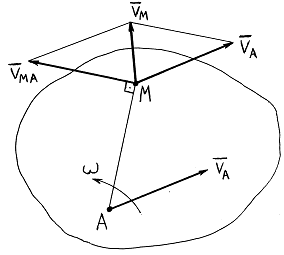
Рассмотрим движение плоской фигуры в плоскости чертежа. Пусть известны скорость 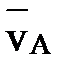 в некоторой точке А и угловая скорость  фигуры. Требуется найти скорость произвольной точки М фигуры. Так как движение фигуры состоит из поступательного движения со скоростью полюса и вращения вокруг этого полюса, то скорость точки М также складывается из скорости 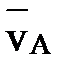 полюса А и скорости  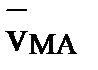вращения точки М вокруг полюса А:

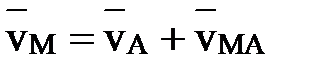                                                                                                  (2)

При этом вектор 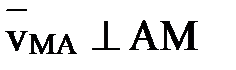 и направлен в сторону , а по величине 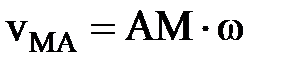 (смотреть тему «Вращательное движение твёрдого тела»). Для сложения  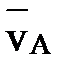и 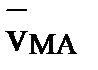 вектор  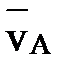параллельно самому себе переносится в точку М и строится параллелограмм.

Таким образом, скорость произвольной точки фигуры равняется векторной сумме скорости полюса и скорости этой точки при вращении вокруг полюса.

Теорема о проекциях скоростей двух точек плоской фигуры.

Спроектируем равенство (2) на прямую АМ:

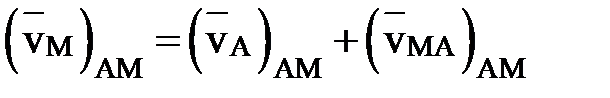
Тогда, учитывая, что 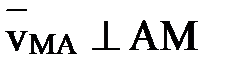, а следовательно 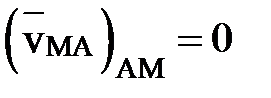, получим

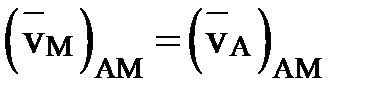                                                                                             (3)

или

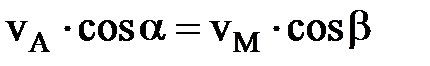                                                                                         (3 ^/)

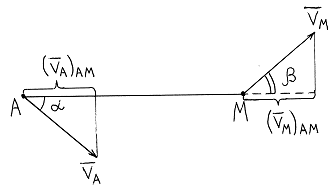
Равенство (3) или (3 ^/) выражает следующую теорему:

В каждый момент времени проекции скоростей произвольных двух точек плоской фигуры на прямую, соединяющую эти точки, равны между собой.

Это положение остаётся справедливым не только при плоском, но и при любом движении твёрдого тела и называется основной теоремой кинематики.

Мгновенный центр скоростей плоской фигуры.