2020-06-29
72
Рассмотрим движение плоской фигуры в плоскости чертежа. Пусть в некоторый момент времени известны ускорение 
некоторой точки А, угловая скорость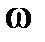 
и угловое ускорение 
фигуры. Требуется найти ускорение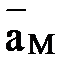 
произвольной точки М фигуры.
Точку А примем за полюс. Так как движение плоской фигуры слагается из поступательного движения, определяемого движением полюса, и вращения вокруг полюса, то и ускорение точки М складывается геометрически из ускорения полюса А и ускорения 
вращения точки М вокруг полюса:
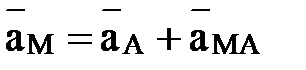
Значение как ускорение точки вращающегося твёрдого тела определяется формулой
Следовательно
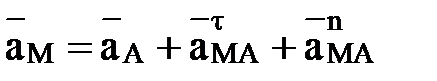
При этом вектор касательного ускорения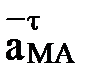 
направлен перпендикулярно отрезку АМ в сторону углового ускорения ; вектор нормального ускорения 
направлен от точки М к полюсу А. Численно же
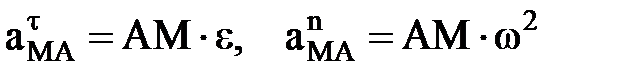
Таким образом, ускорение точки М плоской фигуры геометрически складывается из ускорения полюса и ускорения точки М при вращении вокруг полюса.
Ускорение 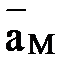точки М можно найти построением соответствую-щего параллелограмма.
