Пусть 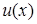 и
и  – функции, которые непрерывны вместе со своими производными на промежутке
– функции, которые непрерывны вместе со своими производными на промежутке 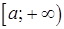 , тогда имеет место формула:
, тогда имеет место формула:
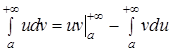 .
.
Пусть 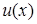 и
и  – функции, которые непрерывны вместе со своими производными на промежутке
– функции, которые непрерывны вместе со своими производными на промежутке 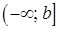 , тогда имеет место формула:
, тогда имеет место формула:
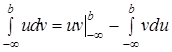 (ср. п. 2.2).
(ср. п. 2.2).
5.2.4. Cходимость несобственного интеграла 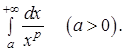
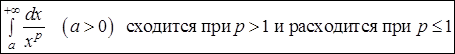 .
.
Признаки сходимости несобственных интегралов
С бесконечными пределами
5.3.1. Пусть для двух непрерывных функций 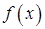 и
и 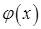 при всех значениях
при всех значениях 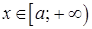 выполняется условие
выполняется условие 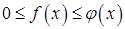 .
.
Тогда:
1) Если сходится 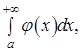 то сходится и то сходится и 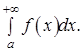 2) Если расходится
2) Если расходится 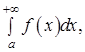 то расходится и то расходится и 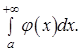
|
5.3.2. Если для двух непрерывных неотрицательных на промежутке 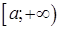 функций выполняется условие
функций выполняется условие
 ( (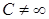 и и 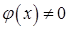 для всех достаточно больших для всех достаточно больших 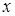 ),
то интегралы ),
то интегралы 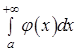 и и 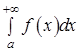 одновременно либо сходятся, либо расходятся. одновременно либо сходятся, либо расходятся.
|
5.3.3. Если на промежутке 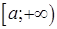 функция
функция 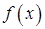 непрерывна и
непрерывна и
 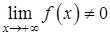 , то несобственный интеграл , то несобственный интеграл 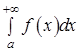 расходится. расходится.
|
5.3.4.Абсолютная и условная сходимость
1) Если 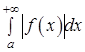 (интеграл от абсолютной величины функции (интеграл от абсолютной величины функции 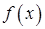 ) сходится, то ) сходится, то 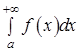 сходится. В этом случае сходится. В этом случае 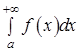 называется абсолютно сходящимся.
2) Если называется абсолютно сходящимся.
2) Если 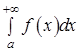 сходится, а сходится, а 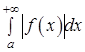 расходится, то интеграл расходится, то интеграл 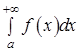 называется условно сходящимся. называется условно сходящимся.
|
 2020-06-29
2020-06-29 92
92








