2020-06-29
67
Основные понятия
5.1.1. Определение. Пусть функция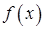 
непрерывна при 
. Несобственным интегралом с бесконечным верхним пределом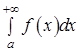 
называется 
.
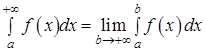Если предел существует и конечен, то несобственный интеграл называется сходящимся, если предел не существует или бесконечен, то интеграл называется расходящимся.
5.1.2. Определение. Пусть функция 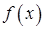непрерывна при 
. Несобственным интегралом с бесконечным нижним пределом 
называется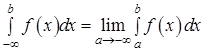 
.
Если предел существует и конечен, то несобственный интеграл называется сходящимся, если предел не существует или бесконечен, то интеграл называется расходящимся.
5.1.3. Определение. Если функция 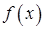непрерывна при 
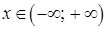, то несобственным интегралом с бесконечными пределами 
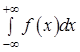называется 
.
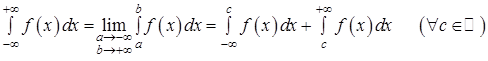Если оба предела существуют и конечны, то несобственный интеграл называется сходящимся, если хотя бы один предел не существует или бесконечен, то интеграл называется расходящимся.
5.1.4. Определение. Главным значением (V.P.) интеграла 
называется 
.
Если несобственный интеграл сходится, то он сходится и в смысле главного значения. Возможны случаи, когда расходящийся интеграл сходится в смысле главного значения.
|
|
|
Вычисление несобственных интегралов с бесконечными
Пределами или установление их расходимости
Формула Ньютона-Лейбница для несобственных интегралов с бесконечными пределами.
1) Если функция 
непрерывна при 
, то 
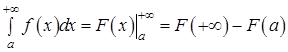, где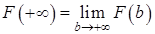 
.
2) Если функция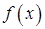 
непрерывна при 
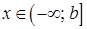, то 
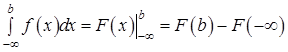, где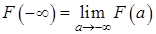 
(ср. п. 1.2.8).
Замена переменной (подстановка) в несобственных интегралах.
Для вычисления несобственных интегралов можно применять замены (см. п. 2.1).
Может случиться, что с помощью замены переменной сходящийся несобственный интеграл превратится в определенный.
