2020-06-29
151
3.4.1. Определить длину окружности радиуса 
, используя ее уравнение в декартовых координатах: 
; в параметрической форме: 
, 
, 
; в полярных координатах: 
.
3.4.2. Вычислить площадь фигуры, ограниченной линиями, уравнения которых 
и 
.
3.4.3. Окружность 
разделена параболой 
на две части. Найти площади обеих частей.
3.4.4. Найти площадь фигуры, ограниченной кардиоидой 
, 
.
3.4.5. Вычислить площадь, описываемую полярным радиусом спирали Архимеда 
при одном его обороте, если началу движения соответствует 
.
3.4.6. Вычислить длину цепной линии 
между точками с абсциссами 
и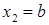 
(
).
3.4.7. Найти длину эвольвенты окружности радиуса 
, 
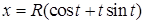от 
до 
.
Ответы. 3.4.1.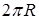 
. 3.4.2. 
. 3.4.3. 
и 
. 3.4.4. 
. 3.4.5. 
. 3.4.6. 
. 3.4.7. 
.
Б)
ВЫЧИСЛЕНИЕ ОБЪЕМА ТЕЛА И ПЛОЩАДИ ПОВЕРХНОСТИ ВРАЩЕНИЯ С ПОМОЩЬЮ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Объемы тел
4.1.1. Вычисление объема тела по площадям поперечных сечений. Пусть дано тело, у которого площадь 
любого сечения, перпендикулярного некоторой оси, которую мы примем за ось 
, является непрерывной функцией от 
Тогда объем этого тела вычисляется по формуле
.
4.1.2. Объем тела вращения. Объем тела, образованного вращением вокруг оси 
криволинейной трапеции, ограниченной двумя прямыми 
и 
, осью и графиком непрерывной на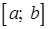 
функции 
вычисляется по формуле
.
Площадь поверхности вращения
4.2.1. Площадь поверхности, образованной вращением дуги гладкой кривой 
при 
вокруг оси , вычисляется по формуле
.
4.2.2. Если кривая задана в параметрической форме 
, 
, 
, причем 
и 
– непрерывно дифференцируемые функции и на отрезке 
выполняются условия 
и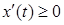 
, то площадь поверхности, образованной вращением этой кривой вокруг оси , определяется интегралом
.
4.2.3. Площадь поверхности, образованной вращением кривой 
, заданной в полярных координатах при 
, вокруг полярного луча, можно найти по формуле
.
